Общее решение исходного уравнения в соответствии с формулой (2) имеет вид
Найдем входящие в это решение интегралы. Имеем
где знаки найденные интегралы в решение (3), окончательно получаем общее решение исходного уравнения:
Из него выделяем частное решение, соответствующее начальному условию у(-2)=2:
Полезно иметь в виду, что иногда дифференциальное уравнение является линейным относительно х как функции у, т.е. может быть приведено к виду
Его общее решение находится по формуле
Пример 3. Найти общий интеграл уравнения ►Данное уравнение является линейным относительно функции х(у). Действительно,
т.е. получили уравнение вида (4). Согласно формуле (5), общее решение исходного уравнения имеет вид
Отметим, что линейное дифференциальное уравнение (1) можно также проинтегрировать методом Бернулли, суть которого заключается в следующем. Введем две неизвестные функции u(x) и v(x) по формуле y=u(x)v(x) (подстановка Бернулли). Тогда
Пример 4. Проинтегрировать уравнение
методом Бернулли и решить задачу Коши при начальном условии ►Сделав подстановку Бернулли
Находим частное решение уравнения
Пологая
Общее решение исходного уравнения
Из него выделяем частное решение, удовлетворяющее начальному условию:
|
(3)
появляются в силу равенства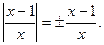 
Подставляя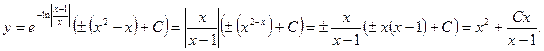
◄
(4)
(5)
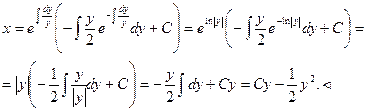
Подставим выражение для 
и 
в уравнение (1), получим уравнение 
которое преобразуем к виду
.
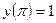получим:
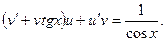
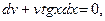
выбираем решение 
Далее ищем общее решение уравнение 
Имеем:
Подставляя значение С=-1 в общее решение, окончательно получим: 
◄
