Уравнение в полных дифференциалах
Определение. Уравнения вида
Общее интеграл уравнения (7) определяется одной из следующих формул:
где точка Пример 3. Найти общее интеграл уравнения ►Ведем обозначения
По формуле (10) получаем общий интеграл:
который совпадает с уже найденным.◄ Аудиторное занятие 1. Указать типы дифференциальных уравнений и методы их решения: а) в) д) ж) з) Найти общий интеграл дифференциального уравнения a) б) в) (Ответ а)
3. Решить задачу Коши: a) б) в) (Ответ: а) Домашнее задание Решить задачу Коши. 1. а) (Ответ: a) 2. a) б) (Ответ: a) 3. a) б) (Ответ: a) 4. Решить задачу Коши:
(Ответ: 5. 1. Найти общий интеграл дифференциального уравнения
6. Найти частное решение дифференциального уравнения
Литература 1. Сборник индивидуальных заданий по высшей математике ч.1-3. Под редакцией Рябушко А.П., Минск: Вышейшая школа, 2001г. 2. Высшая математика в упражнениях и задачах. Ч.1,2 Данко П.Е., Попов А.Г., Кожевников Т.Я., М.: Высшая школа,1986 г. 3. Сборник задач по математике для втузов: Линейная алгебра и основы математического анализа. Под редакцией Ефимова А.В., Демидовича Б.П., М.: Наука, 1986г. 4. Кузнецов Л.А.Сборник заданий по высшей математике (типовые расчеты). М.: Высшая школа, 1983 г.
|

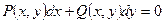 (7) называется уравнением в полных дифференциалах, если в области D определения функций P(x,y), Q(x,y) и существования решений уравнения (7) выполняется равенства
(7) называется уравнением в полных дифференциалах, если в области D определения функций P(x,y), Q(x,y) и существования решений уравнения (7) выполняется равенства (8)
(8) (9)
(9) (10)
(10) .
.
 Так как
Так как  т.е. условие (8) выполнено, то данное уравнение является уравнением в полных дифференциалах. Его общий интеграл можно найти по формуле (9) или (10), положив для простоты
т.е. условие (8) выполнено, то данное уравнение является уравнением в полных дифференциалах. Его общий интеграл можно найти по формуле (9) или (10), положив для простоты 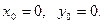 Выбор этих значений
Выбор этих значений  ,
,  допустим, так как функции
допустим, так как функции  и их частные производные определены, т.е. точка
и их частные производные определены, т.е. точка  По формуле (8) имеем:
По формуле (8) имеем:



 ; б)
; б) 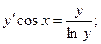
 г)
г) 
 е)
е) 





 )
)


 б)
б)  в)
в)  )
)
 )
)

 )
)

 )
)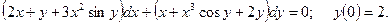
 )
) (Ответ:
(Ответ:  )
) (Ответ:
(Ответ:  )
)


