Различают два рода величин: скалярные и векторные. Если некоторая величина вполне определяется ее числовым значением, то ее называют скалярной (например, масса, плотность, работа, температура). Скаляры являются алгебраическими величинами и с ними можно производить любые алгебраические действия: сложение, вычитание, умножение, деление и т. д. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или вектором (например, скорость, ускорение, сила).
 Графически вектор обозначается отрезком прямой, на котором ставится стрелка, указывающая направление вектора (рис 1.6). Длина, изображающего вектор отрезка, называется длиной вектора, а также его модулем или абсолютной величиной. Обозначается вектор одной буквой с черточкой или стрелкой над ней:
Графически вектор обозначается отрезком прямой, на котором ставится стрелка, указывающая направление вектора (рис 1.6). Длина, изображающего вектор отрезка, называется длиной вектора, а также его модулем или абсолютной величиной. Обозначается вектор одной буквой с черточкой или стрелкой над ней:  или
или  , а модуль этого вектора либо той же буквой, только без черточки над ней, т.е. a, либо
, а модуль этого вектора либо той же буквой, только без черточки над ней, т.е. a, либо  . Также вектор можно обозначать
. Также вектор можно обозначать  , где А – начало и В – конец вектора, а его модуль – теми же буквами, но без черточки наверху. Если модуль вектора равен нулю, то такой вектор называется нулевым и обозначается
, где А – начало и В – конец вектора, а его модуль – теми же буквами, но без черточки наверху. Если модуль вектора равен нулю, то такой вектор называется нулевым и обозначается  .
.
Пример 1.6. Даны точки A (2, 4, 1)и B (–3, –2, 3), найдите векторы  ,
,  и модули этих векторов.
и модули этих векторов.
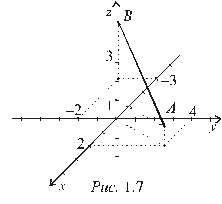 Решение. Если в задаче необходимо «найти вектор», то это означает, что следует определить его координаты. Чтобы определить координаты вектора, надо из координат конца вектора вычесть координаты его начала. Произведем расчет координат вектора
Решение. Если в задаче необходимо «найти вектор», то это означает, что следует определить его координаты. Чтобы определить координаты вектора, надо из координат конца вектора вычесть координаты его начала. Произведем расчет координат вектора  : –3 – 2= –5; –2 – 4 = –6; 3 – 1 = 2, то есть
: –3 – 2= –5; –2 – 4 = –6; 3 – 1 = 2, то есть  (–5; –6; 2). Аналогично,
(–5; –6; 2). Аналогично,  : 2 – (–3) = 5; 4 – (–2) = 6; 1 – 3 = –2, то есть
: 2 – (–3) = 5; 4 – (–2) = 6; 1 – 3 = –2, то есть  (5; 6; –2).
(5; 6; –2).
Модуль вектора  является длиной отрезка AB. Т. е. модуль вектора
является длиной отрезка AB. Т. е. модуль вектора  (x, y, z)в пространстве:
(x, y, z)в пространстве:  . Подставим координаты:
. Подставим координаты:  =
=  ,
,  .
.
Ответ:  (–5; –6; 2),
(–5; –6; 2),  (5; 6; –2),
(5; 6; –2), 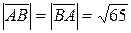 .
.
Равными называют векторы с одинаковой длиной, лежащие на параллельных прямых и направленные в одну и ту же сторону. Координаты равных векторов совпадают. Обратите внимание, что векторы  и
и  (рис.1.7) имеют одинаковую длину, но направлены в разные стороны. Если векторы лежат на одной или параллельных прямых и различны по направлению, такие векторы называют противоположными и обозначают
(рис.1.7) имеют одинаковую длину, но направлены в разные стороны. Если векторы лежат на одной или параллельных прямых и различны по направлению, такие векторы называют противоположными и обозначают  . Координаты противоположных векторов отличаются знаком.
. Координаты противоположных векторов отличаются знаком.
Пример 1.7. Найти вектор, соединяющий точки A (1, 1)и B (3, 3), и его проекции на оси координат плоскости.
 Решение. Проекцией вектора
Решение. Проекцией вектора  на ось
на ось  называется длина отрезка A ¢ В ¢, заключенного между проекциями начала и конца вектора на эту ось (рис.1.8). Этой длине приписывается знак плюс, если направление отрезка A ¢ В ¢ совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси. Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора. Проекция вектора
называется длина отрезка A ¢ В ¢, заключенного между проекциями начала и конца вектора на эту ось (рис.1.8). Этой длине приписывается знак плюс, если направление отрезка A ¢ В ¢ совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси. Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора. Проекция вектора  на ось
на ось  обозначается через
обозначается через 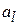 или
или 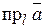 , а угол j между осью и вектором обозначается так:
, а угол j между осью и вектором обозначается так: 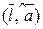 . Таким образом,
. Таким образом, 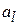 =
= 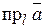 =
=  .
.
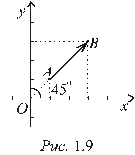 Рассмотрим на плоскости систему координат и изобразим в ней данные точки (рис.1.9). Произведем расчет координат вектора
Рассмотрим на плоскости систему координат и изобразим в ней данные точки (рис.1.9). Произведем расчет координат вектора  : 3 – 1= 2; 3 – 1 = 2, то есть
: 3 – 1= 2; 3 – 1 = 2, то есть  (2; 2). Модуль его равен
(2; 2). Модуль его равен 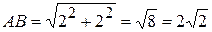 . Видим, что вектор
. Видим, что вектор  лежит на биссектрисе первого и третьего координатных углов, следовательно, образует с каждой из осей угол в 45°. Учитывая, что
лежит на биссектрисе первого и третьего координатных углов, следовательно, образует с каждой из осей угол в 45°. Учитывая, что  , вычислим проекции на оси координат:
, вычислим проекции на оси координат:  ,
, 
 .
.
Обратите внимание, что проекции вектора на оси совпадают с координатами этого вектора.
Ответ:  (2, 2),
(2, 2),  ,
,  .
.

 Графически вектор обозначается отрезком прямой, на котором ставится стрелка, указывающая направление вектора (рис 1.6). Длина, изображающего вектор отрезка, называется длиной вектора, а также его модулем или абсолютной величиной. Обозначается вектор одной буквой с черточкой или стрелкой над ней:
Графически вектор обозначается отрезком прямой, на котором ставится стрелка, указывающая направление вектора (рис 1.6). Длина, изображающего вектор отрезка, называется длиной вектора, а также его модулем или абсолютной величиной. Обозначается вектор одной буквой с черточкой или стрелкой над ней:  или
или  , а модуль этого вектора либо той же буквой, только без черточки над ней, т.е. a, либо
, а модуль этого вектора либо той же буквой, только без черточки над ней, т.е. a, либо  . Также вектор можно обозначать
. Также вектор можно обозначать  , где А – начало и В – конец вектора, а его модуль – теми же буквами, но без черточки наверху. Если модуль вектора равен нулю, то такой вектор называется нулевым и обозначается
, где А – начало и В – конец вектора, а его модуль – теми же буквами, но без черточки наверху. Если модуль вектора равен нулю, то такой вектор называется нулевым и обозначается  .
. и модули этих векторов.
и модули этих векторов.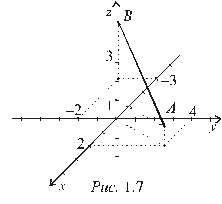 Решение. Если в задаче необходимо «найти вектор», то это означает, что следует определить его координаты. Чтобы определить координаты вектора, надо из координат конца вектора вычесть координаты его начала. Произведем расчет координат вектора
Решение. Если в задаче необходимо «найти вектор», то это означает, что следует определить его координаты. Чтобы определить координаты вектора, надо из координат конца вектора вычесть координаты его начала. Произведем расчет координат вектора  . Подставим координаты:
. Подставим координаты:  =
=  ,
,  .
.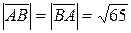 .
. . Координаты противоположных векторов отличаются знаком.
. Координаты противоположных векторов отличаются знаком. Решение. Проекцией вектора
Решение. Проекцией вектора  называется длина отрезка A ¢ В ¢, заключенного между проекциями начала и конца вектора на эту ось (рис.1.8). Этой длине приписывается знак плюс, если направление отрезка A ¢ В ¢ совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси. Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора. Проекция вектора
называется длина отрезка A ¢ В ¢, заключенного между проекциями начала и конца вектора на эту ось (рис.1.8). Этой длине приписывается знак плюс, если направление отрезка A ¢ В ¢ совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси. Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора. Проекция вектора  или
или 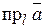 , а угол j между осью и вектором обозначается так:
, а угол j между осью и вектором обозначается так: 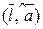 . Таким образом,
. Таким образом,  .
.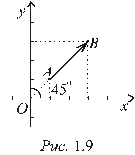 Рассмотрим на плоскости систему координат и изобразим в ней данные точки (рис.1.9). Произведем расчет координат вектора
Рассмотрим на плоскости систему координат и изобразим в ней данные точки (рис.1.9). Произведем расчет координат вектора 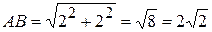 . Видим, что вектор
. Видим, что вектор  , вычислим проекции на оси координат:
, вычислим проекции на оси координат:  ,
, 
 .
. ,
,  .
.


