 Векторным произведением векторов
Векторным произведением векторов  и
и  называется третий вектор
называется третий вектор  (рис. 1.19), если верны следующие условия:
(рис. 1.19), если верны следующие условия:
1.  ;
;
2.  ^
^  и
и  ^
^  ;
;
3.  ,
,  ,
,  образуют правую тройку.
образуют правую тройку.
Обозначается векторное произведение:  ´
´  .
.
Векторное произведение векторов не коммутативно, т. е. нельзя переставлять сомножители векторного произведения.
Пример 1.20. Вычислите векторное произведение векторов  и
и  .
.
Решение. Векторное произведение векторов вычисляется по формуле:  , где
, где 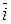 ,
,  ,
, 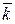 – базисные вектора (орты),
– базисные вектора (орты),  – координаты вектора
– координаты вектора  ,
,  – координаты вектора
– координаты вектора  .
.
В задаче  (–1, 7, 3),
(–1, 7, 3),  (1, 8, –2), значит
(1, 8, –2), значит  . Вычислим определитель:
. Вычислим определитель:  =
=  =
=  . Таким образом,
. Таким образом,  =
=  .
.
Ответ:  (–38, 1, –15).
(–38, 1, –15).
Пример 1.21. Найдите площадь параллелограмма, построенного на векторах  и
и  , как на сторонах.
, как на сторонах.
Решение. Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах, как на сторонах. Действительно,  , а правая часть этого равенства есть формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадь S =
, а правая часть этого равенства есть формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадь S =  .
.
В задаче  (1, –1, 2),
(1, –1, 2),  (2, –3, –1), значит
(2, –3, –1), значит  . Вычислим определитель:
. Вычислим определитель:  =
=  =
=  .
.
Таким образом,  =
=  . Найдем модуль полученного векторного произведения:
. Найдем модуль полученного векторного произведения:  =
=  =
=  . Т. е. площадь параллелограмма равна
. Т. е. площадь параллелограмма равна  масштабных единиц в квадрате.
масштабных единиц в квадрате.
Ответ: S =  кв. ед.
кв. ед.
Пример 1.22. Зная векторы, образующие треугольник ABC:  ,
,  ,
,  , найти длину высоты этого треугольника, опущенной из точки В.
, найти длину высоты этого треугольника, опущенной из точки В.
Решение. Для нахождения длины высоты воспользуемся формулами площади треугольника. С одной стороны площадь треугольника равна половине произведения основания на высоту S =  (рис. 1.20), а с другой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведения S =
(рис. 1.20), а с другой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведения S =  .
.
 Вычислим
Вычислим  =
=  = =
= =  .
.
Найдем модуль полученного векторного произведения: 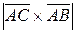 = =
= =  =
=  =
=  . Т. е. площадь треугольника ABC равна
. Т. е. площадь треугольника ABC равна  масштабных единиц в квадрате, S =
масштабных единиц в квадрате, S =  .
.
Найдем длину стороны АС, она равна модулю соответствующего вектора: 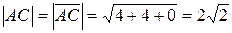 . Тогда
. Тогда  (ед.)
(ед.)
Ответ:  .
.

 Векторным произведением векторов
Векторным произведением векторов  и
и  называется третий вектор
называется третий вектор  (рис. 1.19), если верны следующие условия:
(рис. 1.19), если верны следующие условия: ;
; и
и  .
. , где
, где 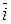 ,
,  ,
, 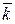 – базисные вектора (орты),
– базисные вектора (орты),  – координаты вектора
– координаты вектора  – координаты вектора
– координаты вектора  . Вычислим определитель:
. Вычислим определитель:  =
=  =
=  . Таким образом,
. Таким образом,  =
=  (–38, 1, –15).
(–38, 1, –15). и
и  , как на сторонах.
, как на сторонах. , а правая часть этого равенства есть формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадь S =
, а правая часть этого равенства есть формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадь S =  .
. . Вычислим определитель:
. Вычислим определитель:  =
=  =
=  .
. =
=  . Т. е. площадь параллелограмма равна
. Т. е. площадь параллелограмма равна  ,
,  ,
,  , найти длину высоты этого треугольника, опущенной из точки В.
, найти длину высоты этого треугольника, опущенной из точки В. (рис. 1.20), а с другой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведения S =
(рис. 1.20), а с другой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведения S =  .
. Вычислим
Вычислим  =
=  = =
= =  .
.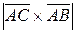 = =
= =  =
=  =
=  . Т. е. площадь треугольника ABC равна
. Т. е. площадь треугольника ABC равна  масштабных единиц в квадрате, S =
масштабных единиц в квадрате, S = 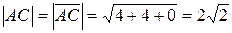 . Тогда
. Тогда  (ед.)
(ед.) .
.


