Координаты точки на плоскости и в пространстве
В настоящих методических указаниях будет рассматриваться только прямоугольная система координат на плоскости и в пространстве. Когда в условии задачи сказано «дана точка», то это значит, что координаты точки известны. Если в задаче необходимо «найти точку», то это означает, что следует определить её координаты. Фраза «дан отрезок прямой» означает, что известны координаты концов этого отрезка. Координаты точки на плоскости записываются в скобках рядом с названием точки, причем всегда на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором – её ордината. Например, если x 1 – абсцисса точки A, а y 1 – ее ордината, то это записывается так: A (x 1, y 1). У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты точки начала координат равны нулю. Для определения местоположения точки в пространстве используются три координаты – абсцисса, ордината и аппликата, это записывается так: A (x 1, y 1, z 1). Пример 1.1. Постройте на плоскости точки A (2, 4)и B (–3, –2), найдите длину отрезка AB. Решение. Выберем единицу масштаба и возьмем на плоскости прямоугольную систему координат. Абсцисса точки A равна 2, а ее ордината 4. Отложим на оси Ox вправо от начала координат О отрезок ОА 1 длиною в 2 единицы масштаба, а по оси Oy вверх от начала координат – отрезок OA 2 длиною 4 единицы масштаба. Из точки А 1 восстановим перпендикуляр к оси Ox, а из точки A 2 – перпендикуляр к оси Oy. Пересечение этих перпендикуляров и определит искомую точку А (рис 1.1).
Расстояние d между точками A (x 1, y 1)и B (x 2, y 2) плоскости определяется по формуле Ответ: Пример 1.2. Постройте на плоскости точки, симметричные точке Решение. Для решения этой задачи следует помнить следующие определения. Две точки M и N называются симметричными относительно прямой, если отрезок MN перпендикулярен этой прямой, причем его середина лежит на этой прямой. Точки M и N называются симметричными относительно точки O, если точка O является серединой отрезка MN.
б) Точка С, симметричная с точкой A (–2, 4)относительно оси Oy, имеет ординату такую же, как и точка А, а абсциссу, равную по абсолютной величине абсциссе точки А, но противоположную ей по знаку (рис. 1.2). Значит, точка С имеет координаты 2 и 4: С (2, 4). в) Точка D, симметричная с точкой A (–2, 4)относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате точки А, но противоположные им по знаку (рис. 1.2). Значит, точка D имеет координаты 2 и –4: D (2, –4). Пример 1.3. Постройте в пространстве точки A (2, 4, 3)и B (1, –3, –2), найдите длину отрезка AB.
Абсцисса точки B равна 1, ее ордината –3, аппликата –2. Отложим на оси Ox вперед от начала координат О отрезок ОВ 1 длиною в 1 единицу масштаба, а по оси Oy влево от начала координат – отрезок OВ 2 длиною 3 единицы масштаба. Через точку В 1 проведем прямую, параллельную к оси Oy, а через В 2 – прямую, параллельную к оси Ox. Пересечение этих прямых определит точку В 3 (рис 1.3), через которую проведем прямую, параллельную оси Oz. Отложим на этой прямой вниз от В 3 – отрезок В 3 В длиною 2 единицы масштаба. Итак, точка B (1, –3, –2) построена. Расстояние между точками пространства определяется по формуле, аналогичной формуле вычисления расстояния между точками плоскости. Расстояние между точками A (2, 4, 3)и B (1, –3, –2) и есть длина отрезка АВ: Ответ: Если даны точки A (x 1, y 1, z 1) и В (x 2, y 2, z 2) в пространстве, то координаты точки С (x, y, z), делящей отрезок АВ в отношении Если l = 1, то точка С (x, y, z) делит отрезок АВ пополам, и тогда координаты середины отрезка: Пример 1.4. Найти точку С – середину отрезка, соединяющего точки A (1, 5, 3)и B (1, –3, –1).
Пример 1.5. Найти координаты центра тяжести однородной пластинки, имеющей форму треугольника с вершинами А (1, 1), В (0, 4) и С (–3, –1) (толщину пластинки не учитывать). Решение. Центр тяжести треугольника находится в точке пересечения его медиан. Из элементарной геометрии известно, что три медианы треугольника пересекаются в одной точке, причем эта точка делит медианы в отношении 2:1, считая от вершины треугольника. Обозначим ее М (x, y). Рассмотрим медиану, проведенную из вершины А. Один ее конец известен А (1, 1), а координаты другого ее конца D получим, как координаты середины отрезка ВС:
Итак, центр тяжести треугольника АВС – точка М
|

 Абсцисса точки B равна –3, а ее ордината –2. Отложим на оси Ox влево от начала координат О отрезок ОВ 1 длиною в 3 единицы масштаба, а по оси Oy вниз от начала координат – отрезок OВ 2 длиною в 2 единицы. Из точки В 1 восстановим перпендикуляр к оси Ox, а из точки В 2 – перпендикуляр к оси Oy. Пересечение этих перпендикуляров и есть точка В (рис 1.1).
Абсцисса точки B равна –3, а ее ордината –2. Отложим на оси Ox влево от начала координат О отрезок ОВ 1 длиною в 3 единицы масштаба, а по оси Oy вниз от начала координат – отрезок OВ 2 длиною в 2 единицы. Из точки В 1 восстановим перпендикуляр к оси Ox, а из точки В 2 – перпендикуляр к оси Oy. Пересечение этих перпендикуляров и есть точка В (рис 1.1). . Расстояние d называется еще длиной отрезка AB. Расстояние между точками A (2, 4)и B (–3, –2) плоскости или длина отрезка АВ равна:
. Расстояние d называется еще длиной отрезка AB. Расстояние между точками A (2, 4)и B (–3, –2) плоскости или длина отрезка АВ равна: 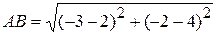

 единиц масштаба.
единиц масштаба. .
. а) Точка В, симметричная с точкой A (–2, 4)относительно оси Ox, имеет абсциссу такую же, как и точка А, а ординату, равную по абсолютной величине ординате точки А, но противоположную ей по знаку (рис. 1.2). Значит, точка В имеет координаты –2 и –4: В (–2, –4).
а) Точка В, симметричная с точкой A (–2, 4)относительно оси Ox, имеет абсциссу такую же, как и точка А, а ординату, равную по абсолютной величине ординате точки А, но противоположную ей по знаку (рис. 1.2). Значит, точка В имеет координаты –2 и –4: В (–2, –4). Решение. Выберем единицу масштаба и возьмем в пространстве прямоугольную систему координат. Абсцисса точки A равна 2, ее ордината равна 4, а аппликата 3. Отложим на оси Ox вперед от начала координат О отрезок ОА 1 длиною в 2 единицы масштаба, по оси Oy вправо от начала координат – отрезок OA 2 длиною 4 единицы масштаба. Через точку А 1 проведем прямую, параллельную к оси Oy, а через A 2 – прямую, параллельную к оси Ox. Пересечение этих прямых определит точку A 3 (рис 1.3), через точку А 3 проведем прямую, параллельную оси Oz. Отложим на этой прямой вверх от А 3 – отрезок A 3 А длиною 3 единицы масштаба. Итак, точка A (2, 4, 3) построена.
Решение. Выберем единицу масштаба и возьмем в пространстве прямоугольную систему координат. Абсцисса точки A равна 2, ее ордината равна 4, а аппликата 3. Отложим на оси Ox вперед от начала координат О отрезок ОА 1 длиною в 2 единицы масштаба, по оси Oy вправо от начала координат – отрезок OA 2 длиною 4 единицы масштаба. Через точку А 1 проведем прямую, параллельную к оси Oy, а через A 2 – прямую, параллельную к оси Ox. Пересечение этих прямых определит точку A 3 (рис 1.3), через точку А 3 проведем прямую, параллельную оси Oz. Отложим на этой прямой вверх от А 3 – отрезок A 3 А длиною 3 единицы масштаба. Итак, точка A (2, 4, 3) построена.
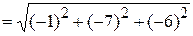
 =
= 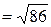 единиц масштаба.
единиц масштаба. .
. определяется по формулам
определяется по формулам  .
. .
.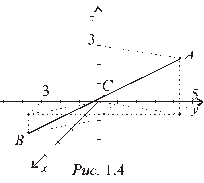 Решение. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Т. е. координаты точки С равны
Решение. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Т. е. координаты точки С равны 

 . Итак, середина отрезка АВ – точка С (1, 1, 1) (рис. 1.4).
. Итак, середина отрезка АВ – точка С (1, 1, 1) (рис. 1.4). .
.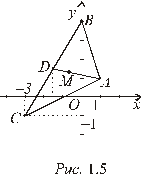 Теперь, зная координаты начала А и конца D отрезка АD и то, что точка М делит этот отрезок в отношении l = 2, получаем
Теперь, зная координаты начала А и конца D отрезка АD и то, что точка М делит этот отрезок в отношении l = 2, получаем  .
.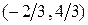 (рис. 1.5). Полученный результат приводит к выводу, что координаты центра тяжести однородной треугольной пластинки, если не учитывать ее толщину, равны среднему арифметическому одноименных координат ее вершин.
(рис. 1.5). Полученный результат приводит к выводу, что координаты центра тяжести однородной треугольной пластинки, если не учитывать ее толщину, равны среднему арифметическому одноименных координат ее вершин.


