СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
При описании процесса автоматического управления реальный объект представляют обычно в виде двух систем: управляющей и управляемой (объекта управления). Структура САУ:
где эндогенные переменные:
Экзогенные (зависимые) переменные:
Для одномерной системы ошибка управления системы Если предписанный закон изменения управляемой величины соответствует закону изменения входного воздействия, т.е. Система управления называется идеальной, если Задачей системы автоматического управления является изменение переменной Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной Свойства систем автоматического управления различных классов можно смоделировать с помощью дифференциальных уравнений и их коэффициентов. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы
Пример: Рассмотрим одноканальную систему автоматического управления SA, которая описывается
где Пусть система SA, работает в некотором режиме малых отклонений от Тогда уравнение (1) можно линеаризовать, разложив функцию
Т.к. уравнение (2) приблизительно описывает рассматриваемый процесс, то производные вычисляются при некоторых фиксированных значениях входящих в него переменных, т.е. мы получаем системы с постоянными коэффициентами. Уравнения получаются линейными относительно Методы решения и исследования линейной системы значительно проще, чем общего вида. Таким образом:
В уравнении (3) для простоты предполагается, что точка приложения возмущающих воздействий совпадает с входом системы (т.е. совпадает с начальной точкой). Решить это уравнение можно, например, операторным методом, значения ДУ алгебраическим (метод конечных разностей). Таким образом, использование Д-схем позволяет формализовывать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход.
ДИСКРЕТНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ ( F-МОДЕЛИ ) На этапе формализации особенности данного подхода можно рассмотреть на примере математического аппарата теории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами. Абстрактно конечный автомат (англ, finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: 1) конечным множеством X входных сигналов (входным алфавитом); 2) конечным множеством Y выходных сигналов (выходным алфавитом); 3) конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); 4) начальным состоянием 5) функцией переходов 6) функцией выходов Автомат, задаваемый F-схемой: Обозначим состояние, а также входной и выходной сигналы, соответствующие такту Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Если Таким образом, работа конечного автомата происходит по следующей схеме: в каждом Получаем: Для F-автомата первого рода (автомат Мили):
для F-автомата второго рода
Автомат второго рода, для которого По числу состояний различают: 1) конечные автоматы с памятью 2) автоматы без памяти (комбинационные или логические схемы) с одним лишь состоянием. Т.е. логическая схема реализует функцию:
это булева функция если алфавиты X и Y состоят из двух букв. По характеру отсчета дискретного времени конечные автоматы делятся на: 1) синхронные – с принудительной синхронизацией. 2) асинхронные - считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое состояние, которое уже не может быть изменено данным входным сигналом. Чтобы задать конечный F-автомат, необходимо описать все элементы множества:
При чем необходимо выделить Существует несколько способов задания работы F-автомата, но наиболее часто используют табличный способ. Табличный способ: Строки соответствуют входным сигналам автомата, столбцы – его состояниям. Обычно первый слева столбец соответствует начальному состоянию z0 . На пересечении i- ой строки и k- го столбца таблицы переходов помещается соответствующее значение Для F-автоматов Мура обе таблицы можно совместить, получая отмеченную таблицу переходов, в которой над каждым состоянием
Таблица 1
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОНЕЧНОГО АВТОМАТА, ЗАДАННОГО НАПРАВЛЕННЫМ ГРАФОМ Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал xk вызывает переход из состояния zi в состояние zj, то на графе автомата дуга, соединяющая вершину zi с вершиной zj, обозначается xk. Для того чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производится так: если входной сигнал xk действует на состояние zi, то, согласно сказанному, получается дуга, исходящая из zi, и помеченная xk; эту дугу дополнительно отмечают выходным сигналом у = y (zi, xk).Для автомата Мура аналогичная разметка графа такова: если входной сигнал xk, действуя на некоторое состояние автомата, вызывает переход в состояние zj то дугу, направленную в zj и помеченную xk, дополнительно отмечают выходным сигналом у = y (zj , xk). Таблица 2
Таблица 3
На рис. 3, а, б приведены заданные ранее таблицами F-автоматы Мили F1 и Мура F2 соответственно.
Рис. 3. Графы автоматов Мили (а) и Мура (6)
При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С= || сij ||, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент cij = xk / ys, стоящий на пересечении i -й строки и j -го столбца, в случае автомата Мили соответствует входному сигналу xk, вызывающему переход из состояния zi в состояние zj, и выходному сигналу ys, вы даваемому при этом переходе. Для автомата Мили F1 матрица соединений имеет вид
Если переход из состояния zi в состояние zj происходит под действием нескольких сигналов, элемент матрицы cij представляет собой множество пар «вход-выход» для этого перехода, соединенных знаком дизъюнкции. Для F-автомата Мура элемент cij равен множеству входных сигналов на переходе (zi, zj), а выход описывается вектором выходов
i- я компонента которого — выходной сигнал, отмечающий состояние zi.
ДИСКРЕТНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Р-СХЕМЫ) Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе к формализации процесса функционирования исследуемой системы S. Так как сущность дискретизации времени при этом подходе остается аналогичной конечным автоматам, то влияние фактора стохастичности проследим также на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах. Основные соотношения. В общем виде вероятностный автомат (англ, probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Применение схем вероятностных автоматов (Р-схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям. Введем математическое понятие Р-автомата, используя понятия, введенные для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (xi, zs), где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции j и y, то с их помощью осуществляются отображения G®Z и G®Y, то говорят, что F =< Z, X, Y, j, y > определяет автомат детерминированного типа. Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида (zk, yj), где уj — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:
При этом
НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-СХЕМЫ)
Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ, queueing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания. Основные соотношения. В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т. д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирования. Остановимся на основных понятиях массового обслуживания, необходимых для использования Q-схем, как при аналитическом, так и при имитационном. В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого i -го прибора обслуживания Пi (рис. 4), состоящего из накопителя заявок Hi, в котором может одновременно находиться
Рис. 2. Прибор обслуживания заявок
Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью { tn } = { Потоком неоднородных событий называется последовательность { tn, fn } где tn — вызывающие моменты; fn — набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок могут быть заданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п.
КОМБИНИРОВАННЫЕ МОДЕЛИ (А-СХЕМЫ) Наиболее известным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Н. П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т. е. по сравнению с рассмотренными является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ, aggregate system), представляющей собой формальную схему общего вида, которую будем называть А-схемой. Основные соотношения. Анализ существующих средств моделирования систем и задач, решаемых с помощью метода моделирования на ЭВМ, неизбежно приводит к выводу, что комплексное решение проблем, возникающих в процессе создания и машинной реализации модели, возможно лишь в случае, если моделирующие системы имеют в своей основе единую формальную математическую схему, т. е. А-схему. Такая схема должна одновременно выполнять несколько функций: являться адекватным математическим описанием объекта моделирования, т. е. системы S, служить основой для построения алгоритмов и программ при машинной реализации модели М, позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования. Приведенные требования в определенной степени противоречивы. Тем не менее в рамках обобщенного подхода на основе А-схем удается найти между ними некоторый компромисс. По традиции, установившейся в математике вообще и в прикладной математике в частности, при агрегативном подходе сначала дается формальное определение объекта моделирования — агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие.
СЕТЕВЫЕ МОДЕЛИ (N-СХЕМЫ) В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри. Основные соотношения. Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное программирование, дискретные динамические системы и т. д.). Формально сеть Петри (N-схема) задается четверкой вида N = < B, D, I, O>, где В — конечное множество символов, называемых позициями, В ¹ Æ; D — конечное множество символов, называемых переходами, D ¹ Æ, BÇ D ¹ Æ; I — входная функция (прямая функция инцидентности), I: B x D ® {0, 1}; О — выходная функция (обратная функция инцидентности), О: D х В ® {0, 1}.
ПОСЛЕДОВАТЕЛЬНОСТЬ РАЗРАБОТКИ И МАШИННОЙ РЕАЛИЗАЦИИ МОДЕЛЕЙ СИСТЕМ С развитием вычислительной техники наиболее эффективным методом исследования больших систем стало машинное моделирование, без которого невозможно решение многих крупных народнохозяйственных проблем. Поэтому одной из актуальных задач подготовки специалистов является освоение теории и методов математического моделирования с учетом требований системности, позволяющих не только строить модели изучаемых объектов, анализировать их динамику и возможность управления машинным экспериментом с моделью, но и судить в известной мере об адекватности создаваемых моделей исследуемым системам, о границах применимости и правильно организовать моделирование систем на современных средствах вычислительной техники. Методологические аспекты моделирования. Сущность машинного моделирования системы состоит в проведении на вычислительной машине эксперимента с моделью, которая представляет собой некоторый программный комплекс, описывающий формально и (или) алгоритмически поведение элементов системы S в процессе ее функционирования, т. е. в их взаимодействии друг с другом и внешней средой Е, Машинное моделирование с успехом применяют в тех случаях, когда трудно четко сформулировать критерий оценки качества функционирования системы и цель ее не поддается полной формализации, поскольку позволяет сочетать программно-технические возможности ЭВМ со способностями человека мыслить неформальными категориями. В дальнейшем основное внимание будет уделено моделированию систем на универсальных ЭВМ как наиболее эффективному инструменту исследования и разработки АСОИУ различных уровней, а случаи использования АВМ и ГВК будут специально оговариваться. Требования пользователя к модели. Сформулируем основные требования, предъявляемые к модели М процесса функционирования системы S. 1. Полнота модели должна предоставлять пользователю возможность получения необходимого набора оценок характеристик системы с требуемой точностью и достоверностью. 2. Гибкость модели должна давать возможность воспроизведения различных ситуаций при варьировании структуры, алгоритмов и параметров системы. 3. Длительность разработки и реализации модели большой системы должна быть по возможности минимальной при учете ограничений на имеющиеся ресурсы. 4. Структура модели должна быть блочной, т. е. допускать возможность замены, добавления и исключения некоторых частей без переделки всей модели. 5. Информационное обеспечение должно предоставлять возможность эффективной работы модели с базой данных систем определенного класса. 6. Программные и технические средства должны обеспечивать эффективную (по быстродействию и памяти) машинную реализацию модели и удобное общение с ней пользователя. 7. Должно быть реализовано проведение целенаправленных (планируемых) машинных экспериментов с моделью системы с использованием аналитико-имитационного подхода при наличии ограниченных вычислительных ресурсов. При машинном моделировании системы 5 характеристики процесса ее функционирования определяются на основе модели М, построенной исходя из имеющейся исходной информации об объекте моделирования. При получении новой информации об объекте его модель пересматривается и уточняется с учетом новой информации, т. е. процесс моделирования, включая разработку и машинную реализацию модели, является итерационным. Этот итерационный процесс продолжается до тех пор, пока не будет получена модель М, которую можно считать адекватной в рамках решения поставленной задачи. Этапы моделирования систем. Рассмотрим основные этапы моделирования системы S, к числу которых относятся: построение концептуальной модели системы и ее формализация; алгоритмизация модели системы и ее машинная реализация; получение и интерпретация результатов моделирования системы. Взаимосвязь перечисленных этапов моделирования систем и их составляющих (подэтапов) может быть представлена в виде сетевого графика, показанного на рис.5.
Рис.5. Взаимосвязь этапов моделирования систем Перечислим эти подэтапы: 1.1—постановка задачи машинного моделирования системы; 1.2 — анализ задачи моделирования системы; 1.3—определение требований к исходной информации об объекте моделирования и организация ее сбора; 1.4 — выдвижение гипотез и принятие предположений; 1.5 — определение параметров и переменных модели; 1.6 — установление основного содержания модели; 1.7 — обоснование критериев оценки эффективности системы; 1.8 — определение процедур аппроксимации; 1.9 — описание концептуальной модели системы; 1.10—проверка достоверности концептуальной модели; 1.11 — составление технической документации по первому этапу; 2.1 — построение логической схемы модели; 2.2 — получение математических соотношений; 2.3 — проверка достоверности модели системы; 2.4 — выбор инструментальных средств для моделирования; 2.5 — составление плана выполнения работ по программированию; 2.6 —спецификация и построение схемы программы; 2.7 — верификация и проверка достоверности схемы программы; 2.8 — проведение программирования модели; 2.9 — проверка достоверности программы; 2.10 — составление технической документации по второму этапу; 3.1 — планирование машинного эксперимента с моделью системы; 3.2 — определение требований к вычислительным средствам; 3.3 — проведение рабочих расчетов; 3.4 — анализ результатов моделирования системы; 3.5 — представление результатов моделирования; 3.6 — интерпретация результатов моделирования; 3.7 — подведение итогов моделирования и выдача рекомендаций; 3.8 — составление технической документации по третьему этапу. Таким образом, процесс моделирования системы S сводится к выполнению перечисленных подэтапов, сгруппированных в виде трех этапов. На этапе построения концептуальной модели Мк, и ее формализации проводится исследование моделируемого объекта с точки зрения выделения основных составляющих процесса его функционирования, определяются необходимые аппроксимации и получается обобщенная схема модели системы S, которая преобразуется в машинную модель Мм на втором этапе моделирования путем последовательной алгоритмизации и программирования модели. Последний третий этап моделирования системы сводится к проведению согласно полученному плану рабочих расчетов ЭВМ с использованием выбранных программно-технических средств, получению и интерпретации результатов моделирования системы S с учетом воздействия внешней среды Е. Очевидно, что при построении модели и ее машинной реализации при получении новой информации возможен пересмотр ранее принятых решений, т. е. процесс моделирования является итерационным.
ПОЛУЧЕНИЕ И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ СИСТЕМ На этапе получения и интерпретации результатов моделирования — ЭВМ используется для проведения рабочих расчетов по составленной и отлаженной программе. Результаты этих расчетов позволяют проанализировать и сформулировать выводы о характеристиках процесса функционирования моделируемой системы S.
Особенности получения результатов моделирования. При реализации моделирующих алгоритмов на ЭВМ вырабатывается информация о состояниях процесса функционирования исследуемых систем z(t)Î Z. Эта информация является исходным материалом для определения приближенных оценок искомых характеристик, получаемых в результате машинного эксперимента, т. е. критериев оценки. Критерием оценки будем называть любой количественный показатель, по которому можно судить о результатах моделирования системы. Критериями оценки могут служить показатели, получаемые на основе процессов, действительно протекающих в системе, или получаемых на основе специально сформированных функций этих процессов. В ходе машинного эксперимента изучается поведение исследуемой модели М процесса функционирования системы S на заданном интервале времени [0, T].Поэтому критерий оценки является в общем случае векторной случайной функцией, заданной на этом же интервале:
Часто используют более простые критерии оценки, например вероятность определенного состояния системы в заданный момент времени t* Î [0, T], отсутствие отказов и сбоев в системе на интервале [О, Т] и т. д. При интерпретации результатов моделирования вычисляются различные статистические характеристики закона распределения критерия оценки. Рассмотрим общую схему фиксации и обработки результатов моделирования системы, которая приведена на рис. 6. Будем рассматривать гипотетическую модель М, предназначенную для исследования поведения системы S на интервале времени [О, Т].В общем случае критерием интерпретации результатов моделирования является нестационарный случайный п- мерный процесс
|


 - векторы входных воздействий;
- векторы входных воздействий; - векторы возмущающих воздействий;
- векторы возмущающих воздействий; - векторы сигналов ошибки;
- векторы сигналов ошибки; - векторы управляющих воздействий.
- векторы управляющих воздействий. - вектор состояния системы
- вектор состояния системы  ;
; - вектор выходных переменных (обычно
- вектор выходных переменных (обычно  ).
). , где
, где  - заданный закон изменения управляемой величины системы;
- заданный закон изменения управляемой величины системы;  - действительный закон изменения.
- действительный закон изменения. (при условии линейной зависимости
(при условии линейной зависимости 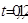 и
и  ).
). во все моменты времени. На практике это не возможно. Таким образом, ошибка
во все моменты времени. На практике это не возможно. Таким образом, ошибка  - неизбежная составляющая объекта автоматического управления, основанного на принципе отрицательной обратной связи. Т.к. для приведения в соответствие выходной переменной
- неизбежная составляющая объекта автоматического управления, основанного на принципе отрицательной обратной связи. Т.к. для приведения в соответствие выходной переменной 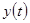 согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы
согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы  , которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе. -схемой общего вида:
-схемой общего вида: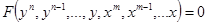 , (1)
, (1) ;
; 
 и
и  , т.е.
, т.е.  и
и  .
. в ряд Тейлора и ограничиться его линейными членами относительно приращений
в ряд Тейлора и ограничиться его линейными членами относительно приращений  и
и  , т.е.:
, т.е.: (2)
(2) (3)
(3) ;
; ;
; .
. — функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
— функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. через
через  ,
,  ,
,  ,
,  ,
,  .
. он всегда находится в начальном состоянии
он всегда находится в начальном состоянии  . В момент
. В момент  , будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал
, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал  , переходя в состояние
, переходя в состояние  .
. ,
,  ,
,  … - это входное, то
… - это входное, то  ,
,  ,
,  … - выходное слово.
… - выходное слово. такте в новое состояние
такте в новое состояние  с выдачей некоторого выходного сигнала.
с выдачей некоторого выходного сигнала.

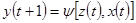

 ,
,  , называется автоматом Мура.
, называется автоматом Мура.
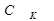

 в момент
в момент 
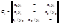 функции переходов, а в таблице выходов – соответствующее значение
функции переходов, а в таблице выходов – соответствующее значение  функции выходов.
функции выходов. автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию выходной сигнал
автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию выходной сигнал  .
.
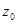









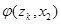







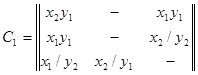 .
.
 , где bkj — вероятности перехода автомата в состояние zk и появления на выходе сигнала yj, если он был в состоянии zs, и на его вход в этот момент времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = < Z, X, Y, B> называется вероятностным автоматом (P-автоматом).
, где bkj — вероятности перехода автомата в состояние zk и появления на выходе сигнала yj, если он был в состоянии zs, и на его вход в этот момент времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = < Z, X, Y, B> называется вероятностным автоматом (P-автоматом). заявок, где
заявок, где 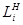 — емкость i -го накопителя, и канала обслуживания заявок (или просто канала) Кi. На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi— поток заявок wi на канал Ki — поток обслуживаний ui.
— емкость i -го накопителя, и канала обслуживания заявок (или просто канала) Кi. На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi— поток заявок wi на канал Ki — поток обслуживаний ui.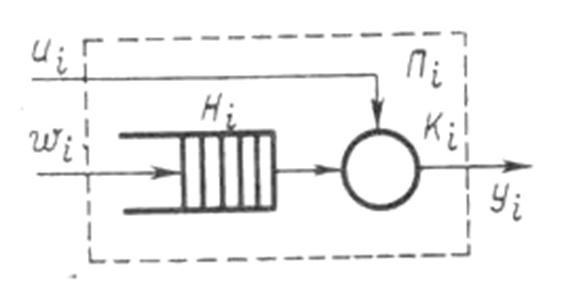
 }, где tn — момент наступления n -го события — неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между n -м и (n-1)-м событиями { tn }, которая однозначно связана с последовательностью вызывающих моментов { tn }, где t = tn - tn - tn-1, n³ 1, t0 = 0, т. е. t1 = t1.
}, где tn — момент наступления n -го события — неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между n -м и (n-1)-м событиями { tn }, которая однозначно связана с последовательностью вызывающих моментов { tn }, где t = tn - tn - tn-1, n³ 1, t0 = 0, т. е. t1 = t1.

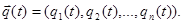
 ,
, 


