МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ
При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преобразованию последовательностей случайных чисел. Моделирование случайных событий. Пусть имеются случайные числа xi т. е. возможные значения случайной величины x, равномерно распределенной в интервале (О, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение xi, случайной величины x удовлетворяет неравенству Тогда вероятность события А будет Процедура моделирования в этом случае состоит в выборе значений xi, и сравнении их с р. При этом, если условие (1) выполняется, исходом испытания является событие А. Таким же образом можно рассмотреть группу событий. Пусть A1, A2, …, As — полная группа событий, наступающих с вероятностями p1, p2, …, ps, соответственно. Определим Аm как событие, состоящее в том, что выбранное значение xi случайной величины x удовлетворяет неравенству
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел xi, со значениями lr. Исходом испытания оказывается событие Аm, если выполняется условие (2). Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p1, p2, …, ps. Эти процедуры моделирования были рассмотрены в предположении, что для испытаний применяются случайные числа xi, имеющие равномерное распределение в интервале (О, 1). При моделировании на ЭВМ используются псевдослучайные числа с квазиравномерным распределением, что приводит к некоторой ошибке. Моделирование непрерывных случайных величин. Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина h задана интегральной функцией распределения
где можно воспользоваться методом обратной функции. Взаимно однозначна монотонная функция Действительно, если случайная величина h имеет плотность распределения
является равномерным в интервале (О, 1). Чтобы получить число, принадлежащее последовательности случайных чисел {уj}, имеющих функцию плотности fn (у), необходимо разрешить относительно yj уравнение
(8) которая описывает условное распределение величины h при условии, что x = xi. Затем определяем конкретное значение
и находим Рассмотрим моделирование непрерывного случайного вектора с составляющими x и h. В этом случае двухмерная случайная величина (x, h) описывается совместной функцией плотности f(х, у). Эта функция может быть использована для определения функции плотности случайной величины как
Имея функцию плотности В соответствии с этой функцией плотности можно определить случайное число уi. Тогда пара чисел (xi, yi) будет являться искомой реализацией вектора (x, h). Рассмотренный способ формирования реализаций двухмерных векторов можно обобщить и на случай многомерных случайных векторов. Однако при больших размерностях этих векторов объем вычислений существенно увеличивается, что создает препятствия к использованию этого способа в практике моделирования систем.
|

 . (1)
. (1)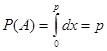 Тогда
Тогда 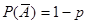 .
. , (2) где
, (2) где 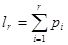 .Тогда
.Тогда 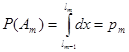 .
.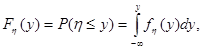
 — плотность вероятностей.
— плотность вероятностей. , полученная решением относительно h уравнения
, полученная решением относительно h уравнения 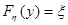 , преобразует равномерно распределенную на интервале (О, 1) величину x в h с требуемой плотностью
, преобразует равномерно распределенную на интервале (О, 1) величину x в h с требуемой плотностью 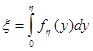
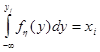 . (7)
. (7)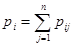 Моделирование случайных векторов. Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, описываемыми совместным законом распределения. Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (x, h) является дискретной и ее составляющая принимает возможные значения x1, x2, …, xn, а составляющая h — значения y1, y2, …, yn, причем каждой паре (xi, yj) соответствует вероятность рij. Тогда каждому возможному значению xi случайной величины x будет соответствовать.
Моделирование случайных векторов. Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, описываемыми совместным законом распределения. Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (x, h) является дискретной и ее составляющая принимает возможные значения x1, x2, …, xn, а составляющая h — значения y1, y2, …, yn, причем каждой паре (xi, yj) соответствует вероятность рij. Тогда каждому возможному значению xi случайной величины x будет соответствовать. Тогда в соответствии с этим распределением вероятностей можно определить конкретное значение xi случайной величины x (по правилам, рассмотренным ранее) и из всех значений pij выбрать последовательность
Тогда в соответствии с этим распределением вероятностей можно определить конкретное значение xi случайной величины x (по правилам, рассмотренным ранее) и из всех значений pij выбрать последовательность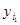 случайной величины h в соответствии с распределением вероятностей. Полученная пара
случайной величины h в соответствии с распределением вероятностей. Полученная пара  будет первой реализацией моделируемого случайного вектора. Далее определяем возможные значения
будет первой реализацией моделируемого случайного вектора. Далее определяем возможные значения 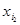 , выбираем последовательность
, выбираем последовательность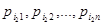 (9)
(9) в соответствии с распределением (9). Это дает реализацию вектора
в соответствии с распределением (9). Это дает реализацию вектора 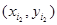 и т. д.
и т. д.
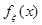 , можно найти случайное число хi, а затем при условии, что x = хi, определить условное распределение случайной величины h:
, можно найти случайное число хi, а затем при условии, что x = хi, определить условное распределение случайной величины h:


