ФОРМАЛЬНАЯ МОДЕЛЬ ОБЪЕКТА
Основними представниками рослинних пігментів є каротиноїди, хлорофіли, госипол (в бавовняній олії). Каротиноїди - природні органічні пігменти, що виробляються бактеріями, грибами, водоростями і рослинами. Вони мають переважно жовтий, помаранчевий або червоний колір, за своєю будовою це циклічні або ациклічні ізопреноїди. Каротиноїди поділяються на 2 групи: 1. Каротини (вуглеводні – α; β; γ -каротини) 2. Кисневмісні каротини (ксантофіли) – похідні каротинів, які можуть являти собою спирти, альдегіди, кетонові кислоти) Каротини є провітаміном вітаміну А, зареєстрований як харчова добавка 160а. Надає колір та запах квітам і рослинам, для людського організму важливий як антиоксидант. Хлорофіли – подвійний ефір спирту фітону та метилового спирту, зелений пігмент, присутній в клітинах рослин, деяких водоростей і ціанобактерій, що надає їм відповідного кольору. Хлорофіл є необхідним для рослин. Він допомагає рослинам отримати з світла енергію.він є необхідним для процесу фотосинтезу. Відіграють важливу роль у внутрішній детоксикації організму, так само як і каротини має антиканцерогенні властивості. Госипол Міститься в насінні бавовнику (5-10 %). Надає бавовняній олії темно-коричневого забарвлення. Цей пігмент токсичний. Відноситься до фенольних сполук.
ОСНОВНЫЕ ПОНЯТИЯ МОДЕЛИРОВАНИЯ СИСТЕМ
В настоящее время в моделировании и синтезе больших систем сложилось два подхода: 1. системный подход; 2. классический подход. Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит ЦЕЛЬ, причем исследуемый объект выделяется из окружающей среды. Структура системы – совокупности связей между элементами системы, отражающих их взаимодействие. Чаще всего структурные связи имеют топологический характер. Системный подход означает, что каждая система S является интегрированным целым даже тогда, когда она состоит из отдельных разобщенных подсистем.
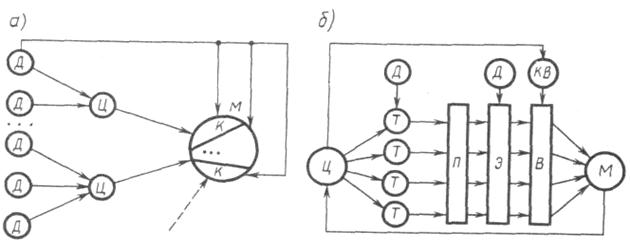
Рис. 2. Процесс синтеза модели на основе классического (а) я системного (б) подходов.
Процесс синтеза моделей М на базе системного подхода состоит в следующем: на основе исходных данных Д, известных из анализа внешней среды (системы), технических ограничений, которые накладываются на систему сверху (верхний иерархический уровень), либо исходя из возможности ее реализаций, и на основе цели функционирования используются/формулируются исходные требования Т к модели системы S. На базе этих требований формируются ориентировочно некоторые подсистемы П, элементы Э и осуществляется наиболее сложный этап синтеза – выбор В составляющих системы, используя специальный критерий выбора КВ. Индуктивный (классический) подход рассматривает систему через переход от частного к общему и синтезирует/конструирует слияния ее компонент, разрабатываемых отдельно. Реальный объект, подлежащий моделированию, разбивается на отдельные подсистемы, т. е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные стороны процесса моделирования. По отдельной совокупности исходных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некоторая компонента К будущей модели. Совокупность компонент объединяется в модель М. Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно независимое рассмотрение отдельных сторон функционирования реального объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличительные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возникновение нового системного эффекта. Моделирование – это зачастую поиск обобщений. Существуют два вида обобщений: 1. дешевый; 2. ценный. Легко обобщать путем разряжения, важно обобщить путем сгущения. На базе системного подхода предполагаются две основные стадии проектирования: 1. Макропроектирование – на основе данных о внешней среде Е и о реальной системе S строится модель внешней среды, выявляются ресурсы и ограничения для построения моделей системы; выбираются модели системы и критерии, позволяющие оценить адекватность модели М реальной системы S. 2. Микропроектирование – более зависит от конкретного типа выбранной модели. В случае имитационного моделирования необходимо обеспечить создание информационного, математического, технического и программного обеспечения. На этой стадии можно установить основные характеристики созданной модели, оценить время работы с ней и затраты ресурсов.
ФОРМАЛЬНАЯ МОДЕЛЬ ОБЪЕКТА Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества: совокупность входных воздействий на систему И совокупность выходных характеристик системы которые являются зависимыми (эндогенными) переменными: Процесс функционирования системы S описывается во времени оператором Fs, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида y(t)=Fs(x, v, h, t). Совокупность зависимостей выходных характеристик системы от времени Весьма важным для описания и исследования системы S является понятие алгоритма функционирования As, под которым понимается метод получения выходных характеристик с учетом входных воздействий Динамические модели – это математические модели, описывающие поведение объекта системы во времени, т.е. отображающие его динамические свойства. Для статических моделей математическая модель представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, Н], что в векторной форме может быть записано как
Соотношения параметров модели, выраженные в определенные моменты времени, называют состояниями (срезами). Состояние системы S характеризуется векторами: Если рассматривать процесс функционирования системы S как последовательную смену состояний z1(t), z2(t),..., zk(t), то они могут быть интерпретированы как координаты точки в k -мерном фазовом пространстве, причем каждой реализации процесса буде соответствовать некоторая фазовая траектория. Совокупность все возможных значений состояний {z} называется пространством состояний объекта моделирования Z, причем zk Î Z. Состояния системы S в момент времени
т.е. Язык моделирования отличается от языка математики тем, что в языке математики состояние системы никого не интересует, т.е. вход® выход. В моделировании вход® состояние® выход, главное состояние. В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, T) как непрерывное, так и дискретное Таким образом, под математической моделью объекта (реальной системы) понимают конечное подмножество переменных Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями Если учитываются стохастические воздействия внешней среды Очевидно, что детерминированная модель является частным случаем стохастической модели.
|

 для всех видов
для всех видов  , иг называется выходной траекторией
, иг называется выходной траекторией  .Зависимость (1) называется законом функционирования системы S и обозначается Fs. В общем случае закон функционирования системы Fs может быть задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.
.Зависимость (1) называется законом функционирования системы S и обозначается Fs. В общем случае закон функционирования системы Fs может быть задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.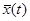 , воздействий внешней среды
, воздействий внешней среды  и собственных параметров системы
и собственных параметров системы 
 полностью определяются начальными условиями
полностью определяются начальными условиями  , где
, где  ; входными воздействиями
; входными воздействиями  и воздействиями внешней среды
и воздействиями внешней среды  и
и  ,
, (вход® состояние® выход).
(вход® состояние® выход).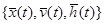 вместе с математическими связями между ними и характеристиками
вместе с математическими связями между ними и характеристиками 


