D) Математичне моделювання в оптимізації
Оптимізація – це вибір найкращого рішення. Математична теорія оптимізації включає в себе фундаментальні результати і численні методи, які дозволяють находити найкращий варіант із більшості можливих альтернатив без їх повного перебору і порівняння. Для того щоб використати результати і обчислювальні процедури теорії оптимізації на практиці, необхідно перш за все сформулювати розглядувану задачу на математичній мові, побудувати математичну модель об’єкта оптимізації. Математична модель – це більш або менш повне математичне описання досліджуваного процесу або явища. Змінними моделі називаються величини Системи обмежень включають систему рівнянь і нерівностей, яким задовольняють змінні моделі і які виходять з обмеженості ресурсів або інших економічних або фізичних умов, наприклад невід’ємності змінних і тому подібне. Цільовою функцією називають функцію змінних моделі, яка характеризує якість рішення задачі, і екстремум якої потрібно знайти. При записі математичних задач оптимізації у загальному виді звичайно використовується наступна символіка:
де У більшості реальних ситуацій дати вичерпуюче математичне уявлення оптимізованої системи з врахуванням всіх взаємозв’язків її частин, взаємодій з внутрішнім світом, усіх цілей її функціонування буває складно чи неможливо. Тому при побудові математичної моделі необхідно, як правило, виділяти і враховувати в майбутньому тільки найбільш важливі, існуючі сторони досліджуваного об’єкта з тим, щоб було можливим його математичне описання, а також наступні рішення поставленої математичної задачі. При цьому невраховані в математичній моделі фактори не повинні істотно впливати на остаточний результат оптимізації. Таким чином, математичне моделювання являється складною і відповідальною творчою задачею, потребуючої від дослідника глибоких знань в відповідній області, практичного досвіду, інтуїції і критичного аналізу отриманих результатів. Математичне моделювання в дослідженні операцій з одного боку є дуже важливим і складним процесом, а з іншого – таким, що практично не піддається науковій формалізації. Варто зазначити, що неодноразові спроби виокремити загальні принципи створеня математичних моделей призводили або до декларування рекомендацій загального характеру, які неможливо використати для вирішення конкретних проблем, або, навпаки, до появи рецептів, які в дійсності можуть бути застосовні тільки до дуже вузького кола задач. Тому більш корисним вважаємо знайомство з технікою математичного моделювання на конкретних прикладах. 1. План постачання підприємства. Нехай маємо ряд підприємств, які використовують різні види сировини, а також ряд баз, ікі постачають сировину. Бази пов’язані з підприємствами різними шляхами сполучення (залізничні шляхи, автотранспорт, водний, повітряний транспорт). Кожний вид транспорту має своі тарифи. Необхідно розробити такий план постачання підприємств сировиною так, щоб потреби у сировині були задоволені при мінімальних витратах на перевезення. 2. Побудова ділянки магістралі. Споруджується ділянка залізнодорожної магістралі. У нашому роспорядженні певна кількість засобів: людей, техніки и т.п. Необхідно призначити черговість робіт, розподілити людей і техніку по ділянкам траси таким чином, щоб завершити будівництво за мінімальні строки. 3. Вибірковий контроль продукції. Випускаєтся певний вид виробів. Для забезпечення високої якості продукції необхідно організувати систему вибіркового контролю: визначити розмір контрольної партії, набір тестів, правила відбракування і т.д. Вимагається забезпечити заданий рівень якості продукції при мінімальніх витратах на контроль. 4. Військові дії. Метою в даному випадку є знищення ворожого об’єкта. На практиці подібні задачі зустрічаються часто. Вони мають загальні риси. В кожній задачі визначена ціль – вони схожі; задані деякі умови – в рамках цих умов і потрібно прийняти рішення, для того, щоб дане міроприємство було б найбільш вигідним. У відповідності з цими загальними рисами застосовуються і загальні методи. Не дивлячись на те, що загального рецепту побудови математичних моделей оптимізації не існує, можна умовно розділити процес математичного моделювання на такі етапи: 1). визчення границь об’єкту оптимізації, вибір змінних задачі; 2). вибір керуючих змінних; 3). визначення обмежень на керуючі змінні; 4). вибір числового критерію оптимізації.
|

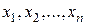 , які повністю характеризують економічний процес, який моделюється. Їх зазвичай записують у вигляді вектора
, які повністю характеризують економічний процес, який моделюється. Їх зазвичай записують у вигляді вектора 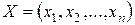 .
.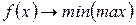 ,
,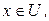
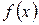 ‑ цільова функція, а
‑ цільова функція, а 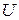 ‑ допустима множина, задана обмеженнями на керуючі змінні.
‑ допустима множина, задана обмеженнями на керуючі змінні.


