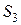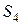J) Типові задачі лінійного програмування
Математичне програмуванння ‑ це сукупність методів прийняття оптимальних рішень на основі знаходженням екстремумів функцій багатьох змінних за наявності обмежень на ці змінні. Методами математичного програмування розв’язуються задачі про розподіл ресурсів, планування випуску продукції, ціноутворенні, транспортні задачі та ін. Серед задач математичного програмування найпростішим (і найкраще вивченими) є так звані задачі лінійного програмування (ЗЛП). Характерним для цих задач є те, що функція Такі задачі досить часто трапляються на практиці, наприклад, при розв’язанні проблем розподілу ресурсів, планування виробництва, керування різноманітними виробничими та технологічними процесами, організації роботи транспорту і т. ін. i) Задача про використання ресурсів (задача планування виробництва) Для виготовлення двох видів продукції Таблиця 1.1.
|
лінійно залежить від розв’язку 
, і обмеження, які накладаються на елементи розв’язку, мають вигляд лінійних рівнянь або нерівностей щодо 
і 
використовують чотири види ресурсів 
. Прибуток від реалізації одиниці продукції 
