E) Формулювання математичної задачі оптимізації
Об’єднуючи результати етапів побудови математичної моделі, її записують у вигляді математичної задачі оптимізації, включаючої побудовану цільову функцію і встановлені обмеження на керуючі змінні. У достатньо загальному виді математичну задачу оптимізації можна сформулювати наступним чином: мінімізувати (максимізувати) цільову функцію з врахуванням обмежень на керуючі змінні. Математичне програмування ‑ це один із інструментів дослідження складних систем (економічної, технологічної, екологічної, соціальної та ін.), який вивчає задачі оптимізації. В економіці такі задачі виникають під час реалізації принципу оптимальності в плануванні та управлінні. Необхідною умовою застосування принципу оптимальності у господарській діяльності є гнучкість, альтернативність ситуацій, в яких доводиться приймати управлінські чи будь-які інші рішення. Суть принципу оптимальності ‑ вибрати таке рішення, яке найкращим чином враховувало б внутрішні можливості та зовнішні умови діяльності економічного суб’єкта. “ Найкращим чином ” ‑ означає, вибір деякого критерію оптимальності, тобто деякого економічного показника, який дозволить оцінити ефективність прийнятого рішення. Наприклад, “максимум прибутку”, “мінімум витрат”, “максимум рентабельності” та ін. “Враховувало б внутрішні можливості та зовнішні умови діяльності” ‑ означає, що на вибір рішення (поведінки) накладається ряд умов, тобто вибір здійснюється із деякої множини можливих (допустимих) рішень Таким чином, реалізувати на практиці принцип оптимальності в плануванні та управлінні ‑ це означає розв’язати екстремальну задачу виду:
де (1.1) – критерій оптимальності;
|
.
, (1.1)
, (1.2)
‑ керовані параметри, які можна змінювати у певних межах (управлінське рішення);
‑ некеровані параметри, значення яких визначаються зовнішніми умовами та характером системи (змінні параметри);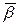
‑ кількісні характеристики системи чи умов (можуть бути незмінними, постійними);
