Vii) Модель «Витрати-випуск» В. В. Леонтьєва
Розглянемо одну із класичних задач дослідження операцій – закриту і стійку модель. Будемо вважати, що об’єкт економічної діяльності випускає
де
Припустимо, що
У деталізованому вигляді матричне рівняння (
де
Якщо технічні коефіцієнти 1. виробничу матрицю 2. матрицю повних витрат 3. матрицю непрямих витрат 4. вектор валового випуску кожної галузі 5. виробничу програму кожної галузі 6. виробничу собівартість
k) Форми запису задачі лінійного програмування (ЗЛП) Усі розглянуті вище задачі, – це задачі на знаходження мінімуму чи максимуму за певних умов. У кожному конкретному випадку умови мали вигляд або нерівностей або рівнянь або одночасно одни і других, а також, як правило, на всі змінні задачі накладались умови невід’ємності, що випливає із природи розглядуваних явищ. Розглянуті задачі мають різний економічний зміст але наділені спільними рисами. Зокрема, у кожній такій задачі потрібно знайти екстремум функції
за обмежень
та умов невід’ємності
Необхідно знайти такий розв’язок системи
|

 найменувань продукції
найменувань продукції  . Крім того
. Крім того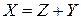 ,
,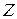 – вектор внутрішнього споживання продукції об’єктом;
– вектор внутрішнього споживання продукції об’єктом;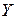 – вектор кінцевої продукції (продукція, яка йде на продаж, запаси тощо).
– вектор кінцевої продукції (продукція, яка йде на продаж, запаси тощо).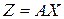 , де
, де  – невід’ємна матриця елементів, які є коефіцієнтами прямих витрат при виробництві продукції. Тоді
– невід’ємна матриця елементів, які є коефіцієнтами прямих витрат при виробництві продукції. Тоді (
(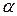 )
)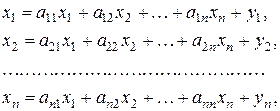 (
( )
) – кількість продукції
– кількість продукції 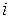 -го виду, потрібної для виробництва одиниці продукції
-го виду, потрібної для виробництва одиниці продукції  -го виду;
-го виду; – компоненти вектора кінцевого випуску;
– компоненти вектора кінцевого випуску;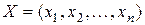 – кількість валового продукту відповідного виду.
– кількість валового продукту відповідного виду.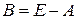 , де
, де 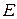 – одинична матриця;
– одинична матриця;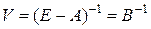 ;
;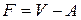 ;
; ;
;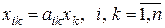 ;
;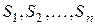 кожного виду продукції за формулою
кожного виду продукції за формулою 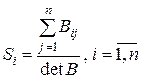 , де
, де 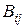 – алгебраїчні доповнення елементів матриці
– алгебраїчні доповнення елементів матриці 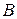 .
. (1.8)
(1.8)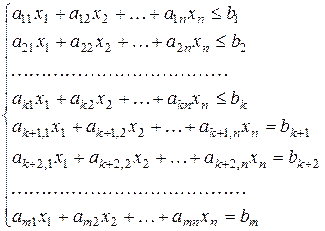 (1.9)
(1.9)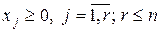 , (1.10)
, (1.10)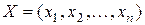 , при якому лінійна функція
, при якому лінійна функція  прийме оптимальне (максимальна чи мінімальне) значення.
прийме оптимальне (максимальна чи мінімальне) значення.


