Математичні основи лінійного програмування. Жорданові перетворенняРозглянемо таку задачу: змінні
Необхідно знайти вирази для Для цього з 1-го рівняння системи (2.4) виразимо
або
Якщо тепер в 2-му рівнянні виразити
і підставити цей вираз в 1-е та 3-є рівняння, отримаємо:
або
І, нарешті, виразивши
підставивши цей вираз у 1-е та 2-е рівняння, отримаємо:
Розв’язуючи цю задачу, можна користуватись простим алгоритмом, що спрощує і прискорює обрахунки. Цей алгоритм називають методом жорданових перетворень таблиць. Із системою лінійних рівнянь
зіставляємо таблицю,
Утворену коефіцієнтами при змінних
|
виражаються через 
таким чином
(2.4)
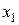через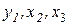 
і підставимо цей вираз у 2-ге і 3-тє рівняння.
через 
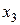через 
,
(2.5)
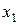
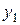
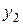
, тобто матрицю 
, стовпець і стрічка, що окреслюють матрицю зліва і зверху, утворені символами 
.У цій таблиці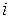 
–му рядку відповідає 
–е рівняння системи.
