Ідея симплекс-методу
Симплес-метод є універсальним, оскільки дозволяє розв’язати практично будь-яку задачу лінійного програмування, записану в канонічній формі. Ідея симплексного методу (методу послідовного покращення плану) полягає в тому, що починаючи з деякого початкового опорного розв’язку здійснюється послідовне направлене переміщення від одного опорного розв’язку задачі до другого і далі до оптимального. Значення цільової функції при цьому переміщенні для задач на максимум не спадає. Оскільки число опорних рішень скінченне, то через скінченне число кроків можна отримати оптимальний розв’язок. Опорним розв’язком називається базисне невід’ємне рішення. Розглянемо задачу лінійного програмування:
Система обмежень (2.7) визначає в
Ця обставина дає можливість не досліджувати на оптимальність всю безмежну множину точок многогранника, а обмежитися перебором його вершин.
Для реалізації цієї ідеї необхідно розробити методику відшукання початкової вершини (опорної), а послідуючий перебір вершин впорядкувати таким чином, щоб на кожному кроці наближатися до оптимального розв’язку. Все це забезпечується спеціальною системою правил. Алгоритм знаходження початкового опорного плану 1. Складаємо початкову жорданову таблицю для задачі (2.6) – (2.8).
Якщо усі (стовпчик вільних членів) додатні, то опорний план знайдено: Якщо 2. Припустимо, що серед вільних членів є від’ємне число 3. Нехай у 4. Для цих пар знаходимо так звані симплексні відношення, поділивши вільний член на відповідний коефіцієнт із рядка 5. Знаходимо найменше симплексне відношення:
6. В якості розв’язуючого елемента приймаємо 7. В сприятливому випадку розв’язуючим елементом може виявитися елемент 8. Аналогічно перетворюємо і всі інші від’ємні елементи стовпчика вільних членів. За скінченне число кроків або отримаємо опорний план, або переконаємося, що задача немає розв’язку. Алгоритм знаходження оптимального плану Нехай маємо опорний план, тобто геометрично – знаходимось у вершині многогранника, а алгебраїчно – це початковий опорний план, яки будемо покращувати.
1. Після отримання опорного плану переглядаємо коефіцієнти рядка функціоналу 2. Якщо у рядку 3. У якості розв’язуючого елемента обирається елемент у розв’язуючому стовпчику, якому відповідає мінімальне симплексне відношення. З цим елементом робимо один крок МЖВ. 4. Отриманий план досліджуємо на оптимальність (п. 1). За наявності 5. Якщо хоча б в одному із стовпчиків, якому відповідає від’ємний елемент у рядку Приклад. Знайти максимум функціоналу
|

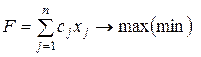 (2.6)
(2.6)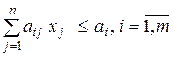 (2.7)
(2.7)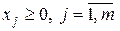 (2.8)
(2.8) випуклий многогранник
випуклий многогранник  , в одній із вершин якого досягається максимум або мінімум функціоналу (2.6).
, в одній із вершин якого досягається максимум або мінімум функціоналу (2.6).

 Тому в основу так званого симплекс-методу розв’язку ЗЛП покладена наступна ідея. Необхідно знайти будь-яку вершину многогранника, а потім здійснювати перехід від вершини до вершини, добираючись до оптимальної вершини.
Тому в основу так званого симплекс-методу розв’язку ЗЛП покладена наступна ідея. Необхідно знайти будь-яку вершину многогранника, а потім здійснювати перехід від вершини до вершини, добираючись до оптимальної вершини.

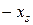
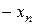

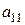

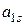
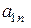
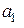
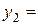
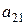

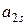
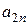
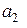
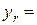
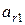
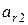
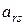
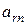

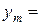
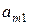
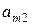
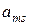
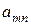

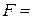

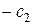
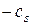

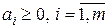 , то
, то 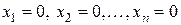 - опорний план
- опорний план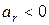 . Проглядаємо стрічку з номером
. Проглядаємо стрічку з номером  . Якщо у цій стрічці всі елементи невід’ємні
. Якщо у цій стрічці всі елементи невід’ємні  , то система обмежень визначає пустий многогранник, нерівності несумісні, задача розв’язку немає.
, то система обмежень визначає пустий многогранник, нерівності несумісні, задача розв’язку немає.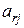 ‑ від’ємний. Таких елементів може бути декілька. Проглядаємо елементи стовпчика з номером
‑ від’ємний. Таких елементів може бути декілька. Проглядаємо елементи стовпчика з номером  і елементи стовпчика вільних членів, порівнюючи їх попарно (в одній стрічці). Фіксуємо тільки ті пари, у яких однакові знаки.
і елементи стовпчика вільних членів, порівнюючи їх попарно (в одній стрічці). Фіксуємо тільки ті пари, у яких однакові знаки.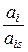 . Отримані симплексні відношення, завжди будуть додатними.
. Отримані симплексні відношення, завжди будуть додатними.
 - елемент
- елемент 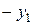
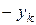
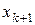
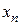
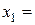

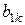

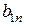


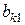
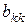
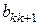



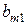
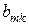
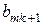

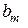
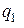

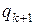
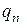

 . Якщо всі
. Якщо всі  окрім
окрім 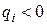 (не враховуючи
(не враховуючи 


