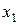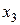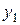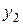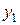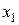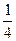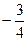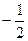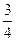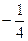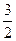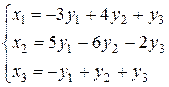Алгоритм жорданових перетворень
1. Виберемо будь-який ненульовий елемент 2. Розв’язуючий елемент замінюємо оберненим 3. Всі елементи розв’язуючого рядка ділимо на розв’язуючий елемент і міняємо знак (крім розв’язуючого елемента). 4. Всі елементи розв’язуючого стовпчика ділимо на розв’язуючий елемент. 5. Решта елементів таблиці переховуємо за «правилом визначника», тобто елемент таблиці
6. Міняємо місцями символи Легко переконатись в тому, що за допомогою жорданових перетворень з розв’язуючими елементами Запишемо вихідну систему у вигляді:
Вибравши розв’язуючий елемент і виконавши один крок жорданових перетворень, отримаємо таблицю:
Виконаємо наступні кроки жорданових перетворень.
Записавши згідно останньої таблиці систему, отримаємо:
|
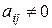і назвемо його розв’язуючим. Називаємо також рядок 
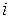таблиці розв’язуючим, а стовпець 
– розв’язуючим стовпцем.
.
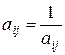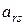замінимо на 
.
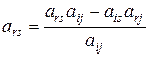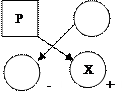
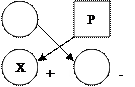
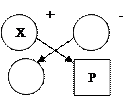Існує чотири випадки розміщення розв’язуючого елемента відносно елемента таблиці, який перераховується: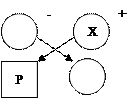
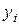та 
.
можна отримати нову таблицю, якій відповідає система m- лінійних рівнянь, де змінні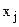 
виражаються через n змінних 
