Приклад 2.1
Розв’язати графічно ЗЛП:
при обмеженнях:
і умовах невід’ємності:
Приведемо в однорідну форму задачу (2.1) –(2.3). Випишемо матрицю коефіцієнтів та за допомогою елементарних перетворень утворимо одиничну підматрицю (віднімемо від першого рядка третій):
Отримаємо еквівалентну систему до системи (2.2)
Очевидно, що одиничну підматрицю утворюють коефіцієнти при змінних
Використовуючи ці залежності виключимо базисні змінні з функціоналу, підставивши їх у вираз функціоналу:
тобто
Після відкидання базисних змінних в системі обмежень отримаємо наступну ЗЛП:
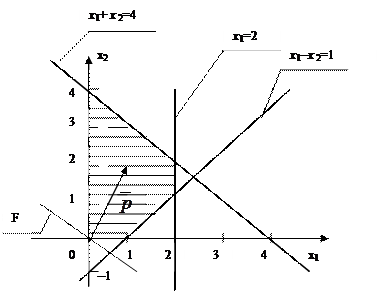
Для графічного розв’язування задачі ( Побудуємо область допустимих розв’язків (ОДР) системи ( (рис. 2.1).
Досліджуючи будь-яку точку (як правило початок координат) з двох півплощин вибирають ту, в якій нерівність має місце. ОДР вибирають як загальну частину (перетин) всіх півплощин, що відповідають обмеженням та умовам невід’ємності. Напрямок зростання цільової функції
Для даної задачі Будуємо вектор Оптимальна точка Оптимальне значення цільової функції для задачі (
Повернувшись до задачі (2.1) – (2.3), отримаємо значення базисних змінних:
Отже оптимальна точка задачі (2.1) – (2.3): Оптимальне значення цільової функції задачі (2.1) – (2.3):
Висновок: задачу(2.1) – (2.3) можна звести до задачі (
|

 (2.1)
(2.1)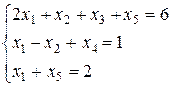 (2.2)
(2.2) (2.3)
(2.3) ~
~ 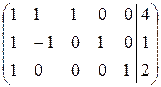
 (
( )
)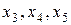 . Отже,
. Отже,  – вільні. Виразимо базисні змінні через вільні:
– вільні. Виразимо базисні змінні через вільні:
 ,
,
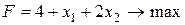 (
( )
) (
( (
( )
)
 вказує її вектор-градієнт:
вказує її вектор-градієнт:
 . Отже
. Отже  .
. і пряму, яка відповідає цільовій функції (вона перпендикулярна до вектора
і пряму, яка відповідає цільовій функції (вона перпендикулярна до вектора 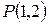 . Знаходимо опорну (оптимальну) точку в ОДР, врахувавши, що лінії рівня (прямі), на яких цільова функція постійна, перпендикулярна градієнту і при переміщенні лінії рівня паралельно самій собі в напрямку градієнта рівень (тобто значення F) збільшується.
. Знаходимо опорну (оптимальну) точку в ОДР, врахувавши, що лінії рівня (прямі), на яких цільова функція постійна, перпендикулярна градієнту і при переміщенні лінії рівня паралельно самій собі в напрямку градієнта рівень (тобто значення F) збільшується. , тобто
, тобто 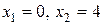 .
.
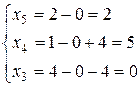
 .
.



