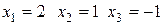Обчислення оберненої матриці за допомогою модифікованих жорданових перетворень
Запишемо умову попередньої задачі у матричному вигляді
Таблиці 4 відповідає рівність
Це означає, що Звідси отримаємо правило обчислення оберненої матриці за допомогою жорданових перетворень: 1. Елементи матриці 2. Позначимо стовпці та рядки символами
Виконаємо Розв’язання систем лінійних рівнянь методом жорданових перетворень Систему лінійних рівнянь
перепишемо у вигляді:
Побудуємо жорданову таблицю:
Проведемо жорданові перетворення, причому поставимо задачу отримати в лівому стовпці символи
Перепишемо цю таблицю, виключивши стовпчик з позначкою 0.
Отже, розв’язки системи:
|

 , де
, де
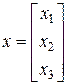

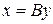 , де
, де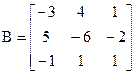
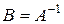 .
. запишемо в жорданову таблицю у звичайному порядку.
запишемо в жорданову таблицю у звичайному порядку.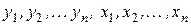 .
.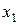



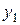
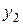

 кроків жорданових перетворень таким чином, щоб
кроків жорданових перетворень таким чином, щоб  помінялись місцями з
помінялись місцями з 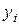 (із збереженням вказаного порядку).
(із збереженням вказаного порядку).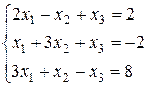
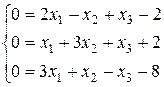
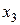
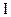
 .
.