Портфельный анализ
Вкладывая средства в различные ценные бумаги, инвестор формирует портфель инвестиций. Он стремится сформировать этот портфель так, чтобы при требуемой им доходности снизить риск либо при данном приемлемом уровне риска повысить доходность. Ожидаемая доходность инвестиционного портфеля определяется как средневзвешенная величина ожидаемых доходностей активов, включенных в портфель: Rp = R1*W1+ R2*W2+… + Rn*Wn, где Ri – доходность i-й ценной бумаги, Wi – доля инвестиций в i-ю бумагу. Риск портфеля в целом измеряется при помощи дисперсии и стандартного (среднеквадратичного) отклонения портфеля. Для расчета дисперсия портфеля, состоящего из n ценных бумаг, используется формула:
где Для случая двух ценных бумаг последнее выражение преобразуется к виду:
Ковариация характеризует взаимосвязь двух случайных величин. Формула для вычисления ковариации имеет примерно такой же вид, как и для вычисления дисперсии:
Где Главное отличие ковариации от дисперсии состоит в том, что в ней присутствуют параметры двух активов Х и У. Ковариация характеризует степень взаимосвязи их изменения. Если активы имеют тенденцию изменяться в одном и том же направлении, то говорят, что они имеют положительную ковариацию, если активы изменяются разнонаправлено, то они имеют отрицательную ковариацию, если они изменяются независимо друг от друга, то ковариация между ними равна нулю. Рассмотрим процедуру расчета ковариации активов А и В (см. табл.)
Процедура расчета ковариации включает расчет среднего значения для каждого актива, отклонений от среднего значения и произведения отклонений. Далее рассчитывается взвешенное по вероятности произведение отклонений и значение ковариации. Ковариация является показателем взаимосвязи двух переменных. В данном примере она является положительной. Это означает, что доходность активов А и В имеет тенденцию изменяться в одном направлении. Проблема использования показателя ковариации состоит в сложности содержательной интерпретации его числового значения. В связи с этим наибольшее практическое применение получил такой показатель взаимозависимости двух переменных, как коэффициент корреляции, который определяется из следующего соотношения: CRxy = где Коэффициент корреляции является нормированным показателем и его значение лежит в диапазоне от -1 до +1. Если CR xy = -1, то это означает, что значения доходности активов изменяются строго в противоположных направлениях, а ели - +1, строго в одном направлении. Значения коэффициента корреляции, находящиеся между двумя крайними значениями характеризует определенный уровень взаимосвязи между ценными бумагами. В нашем примере коэффициент корреляции равен CRав = Таким образом, активы А и В имеют примерно одинаковый характер изменения, т.е. между ними существует сильная взаимосвязь. Рассчитаем показатели дисперсии и стандартного отклонения портфеля при условии равенства удельных весов ценных бумаг в портфеле
Таким образом, в данном примере стандартное отклонение портфеля находится в интервале между стандартными отклонениями активов А и В.
|

 2 =
2 = 

 Wi * Wj,
Wi * Wj,
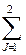
 *W12 +
*W12 +  *W22 +2*
*W22 +2*  *W1* W2
*W1* W2 =
=  (Rxк - Rcx)*(Ryк - Rcy)*Pi,
(Rxк - Rcx)*(Ryк - Rcy)*Pi, ),
), в/(
в/(  ) = 0, 0014/(0, 3225*0, 04583) = 0, 95
) = 0, 0014/(0, 3225*0, 04583) = 0, 95 2 Wx2 +
2 Wx2 +  2 Wу2 +2*(
2 Wу2 +2*(


