Где – ковариация ценных бумаг i и jВ качестве ограничения выступаетсредняя доходность портфеля Rр = где Ri, Wi– доходность и удельный вес включенной в портфель i – ой ценной бумаги. При этом сумма удельных весов бумаг должна быть равна 1, т.е. Для того, чтобы найти решение такой задачи вводят набор переменных λ 1 и λ 2, называемых множителями Лагранжа и составляется функция Лагранжа: L = где λ 1, λ 2— множители Лагранжа. Структура портфеля, имеющего минимизирующий риск, определяется решением системы уравнений: dL/dWi =0 dL/d λ к, =0. где к = 1, 2. Данная система уравнений представляет собой модель, позволяющая определить структуру оптимального портфеля. Пример. Необходимо сформировать портфель из двух ценных бумаг Альфа и Омега, обладающий минимальным риском. Бумаги имеют следующие показатели доходности и риска: RА = 12%, RО = 5.1%, L = dL/dWА = 2 dL/dW2 = 2 dL/d λ 1, = RАWА + RОWО – Rр = 0. dL/d λ 2, = WА+. WО - 1 =0 Представим данную систему уравнений в матричном виде:
Если обозначить матрицу через Н, вектор – через А и вектор в правой части – через G, то получим уравнения в матричной форме: Н*А = G, А = Н-1* G.
Рассмотрим далее задачу для случая портфеля состоящего из трех ценных бумаг: L = dL/dW1 = 2 dL/dW2 = 2 dL/dW3 = 2 dL/d λ 1, = R1W1 + R2W2 + R3W3 – Rр = 0. dL/d λ 2, = W1+. W2 W3 - 1. Представим данную систему уравнений в матричном виде:
Если обозначить матрицу через Н, вектор – через А и вектор в правой части – через G, то получим уравнения в матричной форме: Н*А = G, А = Н-1* G. Пример. Имеются три акции. Их параметры представлены в таблице
Матрица Н G и Н-1 для данной задачи будет иметь следующий вид
Удельные веса акций будут равны
Если инвестор хочет получить доходность Rр = 12%, то получим: W1 = 0, 305, W2 = 0, 259, W3 = 0, 435. Рассмотренный пример иллюстрирует вычислительные трудности, связанные с использованием модели Марковица. Так сам Марковиц подсчитал, что анализ 100 ценных бумаг требует вычисления 100 ожидаемых значений доходности, 100 дисперсий и почти 5000 ковариаций. В связи с этим уже 1962 корпорацией IBM была разработана первая компьютерная программа для реализации модели Марковица.
|
RiWi,
Wi * Wj +λ 1 *( 
= 21.1%, 
= 8.3%., коэффициент корреляции равен 0.18. Доходность портфеля Rр должна составлять 8.9%. Функция Лагранжа для данной задачи будет иметь вид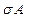
*WА2 + 
**WО2 +2*WА * WО* 
+ λ 1 *(RАWА + RОWО – Rр)+ λ 2 *(WА+. WО – 1).
*W12 + 
*W22 +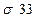 
*W32 +2*W1 * W2* 
+2*W1 * W3* 
+2*W2 * W3* 
+ λ 1 *(R1W1 + R2W2 + R3W3 – Rр)+ λ 2 *(W1+. W2 W3 – 1).
+ λ 1 * R3 + λ 2
= -0, 1
= 0, 42
= 0, 30
