Модель оценки капитальных активов

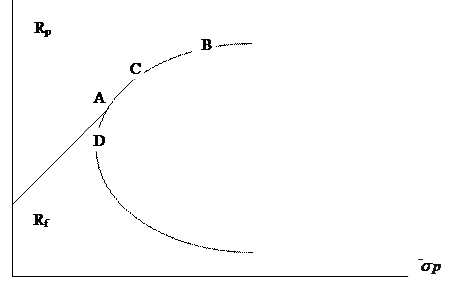
Выше было показано, как формируется портфель, состоящий из рисковых активов. Инвестор, однако, может создать портфель, включающий наряду с рисковыми и безрисковый актив. Этот актив имеет нулевой риск и некоторую безрисковую доходность, которую обозначим через R_f (см. рис.). Точка R_f соответствует ситуации, когда портфель сформирован только из безрисковых активов. Комбинация безрискового и рискового актива упрощает зависимость между риском и доходностью портфеля. Точка А соответствует ситуации, когда портфель составлен только из рисковых активов. Возможные портфели сформированные из комбинации рисковых и безрисковых активов будет располагаться на прямой, соединяющей точку безрисковой доходности и точку А пересечения этой линией эффективного множества рисковых портфелей. Вид линии R_fА обусловлен отсутствием корреляционной зависимости между безрисковым активом с одной стороны и рисковым активом с другой, т.е. при комбинации рисковых и безрисковых активов эффект диверсификации не возникает.

Рассмотренное взаимоотношение между риском и доходностью известна как модель оценки капитальных активов (capital asset pricing model CAPM). В соответствии с моделью CAPM инвесторы формируют портфель не только из рисковых активов, а определяют доли средств направляемых в рисковые и безрисковые активы. Точки на прямой R_fА находящиеся вблизи точки А соответствуют портфелям, сформированным в основном их рисковых активов, а вблизи точки R_f – из безрисковых.

 

Рис. Достижимое множество портфелей в модели CAPM

 

Выбор соотношения между риском и доходностью в рамках модели CAPM существенно отличается от модели Марковица. В рамках последней модели инвесторы ищут конкретный портфель рисковых активов, соответствующий их отношению к риску. В рамках модели CAPM (Capital asset pricing model) инвестор определяет риск портфеля путем выбора соотношения между рисковыми и безрисковыми активами. Так, например, инвесторы менее склонные к риску большую часть своих средств помещают в государственные ценные бумаги, а более терпимые к риску – в корпоративные ценные бумаги.

На представленном выше рисунке можно провести сотни линий, соединяющих точку R_f и линию эффективных портфелей. Из них необходимо выбрать такую, которая является наилучшей для инвестора, т.е. обеспечивает наилучшее соотношение между доходностью и риском.

Так например портфели, лежащие на линии R_fА не являются эффективными, так как любому портфелю, лежащему на этой линии может быть противопоставлен портфель с большей доходностью при том же самом уровне риска. Например, портфель Р2 имеет более высокую доходность при том же уровне риска.

 

Следовательно, эффективные портфели будут лежать на линии, которая имеет наибольший наклон по отношению к горизонтальной оси. Эта линия выходит из точки R_f и является касательной по отношению к кривой, соответствующей эффективному множеству в модели Марковица. Портфели, лежащие на прямой R_fМ обеспечивают наибольшую доходность при заданном уровне риска.

Эта единственную линию называют линией рынка капитала (Capital Market Line). Точка М соответствует рыночному портфелю, т.е. портфелю составленному из всех рисковых активов. Каждый актив в рыночном портфеле представлен в пропорции соответствующий его доли на рынке. Так, например, на фондовом рынке США доля компании General Motors составляет один процент рисковых активов. Исходя из этого доля акций данной компании в рыночном портфеле также должна составлять один процент.

Уравнение линии рынка капитала имеет следующий вид

R_p = R_f + [(R_m - R_f)/ ]* ,

Где R_p – ожидаемая доходность портфеля, состоящего из рисковых и безрисковых активов, величина (R_m - R_f)/ характеризует тангенс угла наклона линии рынка капитала.

Ранее нами были рассмотрены понятия систематического (недиверсифицируемого) и несистематического (диверсифицируемого) риска. Для измерения систематического риска используется показатель бета. Нулевое значение бета соответствует отсутствию систематического риска, а бета равное единице - систематическому риску рыночного портфеля. Если известен показатель бета актива, то его доходность в рамках модели CAPM может быть определена из следующего соотношения:

R_i = R_f + β _i * (R_m - R_f),

Где R_i – ожидаемая доходность актива, R_m, R_f – доходность рыночного портфеля и безрисковая доходность, β _i – бета коэффициент актива.

Бета коэффициент акций или других ценных бумаг рассчитывается как отношение ковариации актива и рыночного портфеля и дисперсии рыночного портфеля:

β _i = / ².

Числитель представляет вклад индивидуального актива I в величину риска диверсифицированного портфеля, а знаменатель – величину риска рыночного портфеля. Таким образом, бета измеряет систематический риск относительно риска рынка в целом.

Пример. Рассмотрим процедуру вычисления бета коэффициента на примере компании Макдоналдс. В колонках 2 и 3 представлены данные по годовой доходности за 9 лет для акций компании Макдоналдс и для рынка в целом. В колонках 4 и 5 представлены разности между текущей доходностью и средней доходностью. Так, например, значение -0, 1113 в колонке 4 для 1977 года получается путем вычитания из доходности акций Макдоналдс в 1997 году равной -0, 0388 среднего значения доходности равной 0, 0725. В колонке 6 представлены квадраты отклонения ежегодной доходности рынка от среднего значения, а в колонке 7 – произведения ежегодных отклонений доходности акций Макдоналдс и рынка.

 

Год	Доходность МД Rmd	Доходность рынка Rm	Отклонение МД (Rmd-Rcmd)	Отклонение рынка (Rm-Rcm)	Квадрат отклонения рынка (Rm-Rcm)2	Произведение отклонений (Rmd-Rcmd)* (Rm-Rcm)
	-0, 0388	-0, 0392	-0, 1113	-0, 1153	0, 0133	0, 0128
	-0, 1019	-0, 0204	-0, 1744	-0, 0965	0, 0093	0, 0168
	-0, 0620	0, 0729	-0, 1345	-0, 0032		0, 0004
	0, 1238	0, 1553	0, 0513	0, 0792	0, 0063	0, 0041
	0, 3411	0, 0756	0, 2686	-0, 0005		-0, 0001
	-0, 0765	0, 0625	-0, 1490	-0, 1386	0, 0192	0, 0207
	0, 1676	0.3416	0, 0951	0, 2655	0, 0705	0, 0252
	-0, 2677		-0, 3402	-0, 0761	0, 0058	0, 0259
	0, 5665	0, 1615	0, 4902	0, 0854	0, 0073	0, 0422
Среднее	0, 0725	0, 0761
Всего					0, 1317	0, 1480

 

Ковариация доходности акций Макдоналдс и рынка будет равна

CV(Rmd, Rm) = 0, 1480/9 = 0, 0164.

Далее определяем дисперсию рынка.

². = 0, 1317/9 = 0, 0146.

Бета коэффициент акций Макдоналдс найдем из следующего соотношения:

β _i = CV(Rmd, Rm) / ² = 0, 0164/0, 0146 = 1, 123

Коэффициент бета ( -коэффициента) характеризует склонность актива «двигаться» вместе со всем рынком. Иными словами характеризующего степень ее изменчивости по отношению к «средней акции», в качестве которой рассматривается акция, стремящаяся «двигаться» синхронно со всем рынком акций.

Это означает, что если доходность по рынку в целом увеличивается на 10%, то доходность «средней акции» возрастает в такой же степени, и, наоборот – при падении – падает. Портфель акций с - коэффициентом, равным единице, будет иметь такую же степень риска, как и весь рынок. Если для акции = 0, 5, это означает, что ее доходность будет повышаться или падать вдвое меньше, чем у всего рынка. Портфель акций с таким -коэффициентом будет иметь вдвое меньшую степень риска по сравнению с портфелем, имеющим =1. В то же время если акция имеет = 2, то ее подвижность вдвое выше, чем у средней акции.

Важным свойством - коэффициента является то, что портфеля вычисляется как взвешенная сумма - коэффициентов составляющих его активов. При этом следует помнить, что общий риск портфеля не является взвешенной суммой составляющих его активов. Обусловлено это тем, что бета измеряет только систематический риск актива, который не является диверсифицируемым.

Исходя из вышесказанного для расчета -коэффициента портфеля акций может быть использовано следующее соотношение

_p = ₁*W₁+ ₂*W₂+… + _n*W_n,

Например, инвестор имеет 40 тыс. долл. и сформировал портфель из четырех акций, вложив в каждый вид акций по 10 тыс. долл. Если каждая акция имеет = 0, 8, то бета такого портфеля также будет равен 0, 8:

_p = 0, 8 х 0, 25 + 0, 8 х 0, 25 + 0, 8 х 0, 25 = 0, 8.

Такой портфель будет менее рисковым, чем весь рынок акций, и будет испытывать меньшее колебание доходности по сравнению со всем рынком. Теперь представим, что одна из акций продана и заменена акцией, имеющей = 2, тогда риск портфеля увеличится и его бета возрастет:

_p = 0, 8 х 0, 25 + 0, 8 х 0, 25 + 0, 8 х 0, 25 + 2, 0 х 0, 25 =1, 1.

Если одну из акций заменить на акцию с = 0, 2, то бета портфеля снизится и составит:

_p = 0, 8 х 0, 25 + 0, 8 х 0, 25 + 0, 8 х 0, 25 + 0, 2 х 0, 25 = 0, 65.

Таким образом, риск портфеля может быть снижен путем включения в портфель акций, имеющих низкое значение -коэффициента.

В таблице представлены - коэффициенты некоторых отечественных и зарубежных компаний.

Компания
American Express	1, 35
Ford Motor	1, 26
K mart	1, 15
General Electric	1, 09
Procter& Gamble	0, 8