Оптимизация портфеля, состоящего из двух ценных бумаг
Как было показано ранее доходность и среднеквадратичное отклонение портфеля, состоящего из двух активов определяется следующими соотношениями: Rp = R1*W1+R2*W2
Рассмотрим задачу определение структуры портфеля, обеспечивающего минимальный уровень риска. Обозначим за W – доля актива Х в портфеле, тогда (1- W) будет доля актива У. С учетом этого выражение для стандартного отклонения портфеля будет иметь вид:
При заданных значениях
2*( Из данного выражения получаем W = ( Полученное выражение позволяет определить удельный вес активов в портфеле, обеспечивающий минимальный риск. Рассмотрим ряд частных случаев. 1. Между активами имеет место наибольшая отрицательная ковариация, т.е CRxy = -1. Выражение для удельного веса актива Х в этом случае будет иметь вид W = ( 1- W = Для нахождения среднеквадратичного отклонения портфеля необходимо подставить полученные выражения для удельных весов активов в исходное выражение для
Таким образом, при абсолютной отрицательной ковариации между активами можно определить такие их удельные веса, что риск портфеля будет равен нулю. 2. Рассмотрим далее случай ковариации активов равной нулю, т.е. CRxy = -0. Подставляя в выражение W = ( CRxy = -0, Получим W = ( 1- W = ( Риск портфеля в этом случае будет равен
2. Третий случай будет соответствовать абсолютной положительной ковариации активов Х и У. Подставим в выражение W = ( CRxy = 1, Получим W = 1- W = - Минимальный риск портфеля в этом случае достигается при отрицательном удельном весе одного из активов в портфеле. Пример. Рассмотрим две ценные бумаги Х и У. Их среднемесячная доходность представлена в таблице.
Средняя доходность активов Х и У будет равна: Rcx = (5, 5+8, 1+6, 2+3, 4+8, 5+6, 0+7, 0+5, 0+8, 0+9, 0+9, 5+7, 5)/12 = 7, 0 Rcу = (10+30+20+40+25+10+5+30+10+15+50+20)/12 = 22, 1 Среднеквадратичное отклонение доходности ценных бумаг и коэффициент корреляции равны:
Доходность и риск портфеля в зависимости от вариантов его формирования представлены в таблице: Варианты портфелей ценных бумаг Х и У
|

 = (
= ( 2*Wх2 +
2*Wх2 + 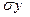 2*Wу2 +2*Wх* Wу*
2*Wу2 +2*Wх* Wу*  (2*
(2* 


