Цена опциона, модель Блека—Шоулза
Как было показано выше, реальные прибыль или потери от опциона для обеих участвующих сторон зависят от цены исполнения, рыночной цены актива на момент исполнения опциона и премии. В условиях развитого рынка опционов цена исполнения устанавливается на бирже опционов. Обычно это величина, близкая к текущей рыночной цене актива. Если биржа опционов отсутствует, то единственный путь установления цены исполнения — непосредственная договоренность покупателя и продавца опциона. Предлагаемая продавцом цена должна быть конкурентоспособной и в то же время обеспечить ему некоторую прибыль. Опционы представляют определенный интерес не только в практическом плане, но и в теоретическом — с позиции количественного анализа, который осуществляется с помощью разработки специальных моделей (option models), описывающих взаимосвязи основных параметров опционов. Следует, однако, заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена относительно теоретической цены, то есть основание для его покупки. Наиболее известной моделью определения цены опциона является модель Блека—Шоулза (Black—Scholes). Рассмотрим ее применительно к опционам колл для обыкновенных акций. Ранее мы говорилось о том, что цены опционов определяются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К их числу следует отнести: · текущая цена базисного инструмента, · уровень цены исполнения, · стандартное отклонение доходности базисного инструмента, · срок исполнения опциона, · размер безрисковой ставки. Одной из наиболее важных зависимостей в моделях ценообразования опционов является зависимость между ценной опциона и ценой базисного актива.
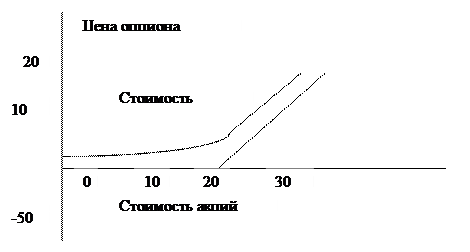
При низкой стоимости базисного актива относительно цены исполнения цена опциона является также низкой и имеет тенденцию незначительного роста при росте стоимости базисного актива. На данном рисунке цена исполнения опциона составляет 20 рублей. Если цена акций растет, но остается существенно меньшей цены исполнения, то это не приводит к существенному росту цены опциона. Если цена акций существенно превышает цену исполнения, то цена опциона изменяется в соответствие с изменением цены базисного актива. Вторым параметром, определяющим цену опциона, является цена его исполнения. Она остается постоянной в течение времени жизни опциона. В модели Блека—Шоулза цена опциона и цена исполнения связаны обратной зависимостью. Обусловлено это тем, что опцион становится прибыльным только в том случае, если цена базисного актива превышает цену исполнения. Третьим параметром является стандартное отклонение доходности базисного актива. В модели Блека—Шоулза цена опциона возрастает при росте стандартного отклонения и соответственно риска базисного актива. Такой характер зависимости обусловлен тем, что опцион является финансовым инструментом с неограниченным потенциалом прибыльности при ограниченных возможностях потерь. В результате при возрастании изменчивости (волатильности) базисного инструмента возможности получения большей прибыли увеличиваются. При этом возможные потери остаются на прежнем уровне. Четвертым параметром в модели Блека—Шоулза является срок исполнения опциона. Поскольку большинство опционов позволяют их держателям исполнить опцион в любой момент в течение срока его жизни, то их цена связана со сроком исполнения прямой зависимостью. Более длительный срок исполнения создает большие возможности для повышения цены базисного актива. Последним параметром в модели Блека—Шоулза является размер безрисковой ставки. Для понимания влияния данного параметра на цену опциона рассмотрим следующий пример. Предположим, что вы ожидаете рост стоимости акций в будущем и решили их приобрести. Инвестиции при этом могут быть произведены как в сами акции, так и в опцион на их приобретение. Если вы инвестируете средства в акции, то ваши инвестиции будут соответствовать текущей стоимости акций. Если вы приобретаете опцион, то текущие инвестиции будут равны цене опциона, а будущие – цене исполнения. Таким образом при приобретении опциона вы фактически откладываете оплату приобретаемых акций на будущее. В результате при повышении безрисковой ставки эффективность приобретения опциона увеличивается. Все названные факторы учитываются в формуле Блека—Шоулза. CALL = P* N(d1) – E*e-rt * N(d2) Где: CALL — цена опциона, P — текущая цена акции, Е — цена исполнения, e-rt — дисконтный множитель на срок t по непрерывной ставке? t — срок до даты исполнения, r — непрерывная процентная ставка, принятая для дисконтирования, N(d1) и N(d2) — функции нормального распределения, d1 = [ln(P/E)+(r+0, 5* d2 = d1 - Величина E*e-rt представляет собой дисконтированную на момент покупки опциона цену исполнения. Функции нормального распределения (плотности вероятности) определяются для параметров d1 и d2. Пример 1. Колл опцион дает право на приобретение акций компании А по цене 20 рублей за штуку. До срока исполнения остается 0, 5 года. Безрисковая ставка равна 5% и стандартное отклонение доходности акций составляет 0, 3. Стоимость акций в настоящее время составляет 25 рублей за штуку. Необходимо определить цену опциона. Шаг 1. Рассчитываем значения величин d1 и d2. d1 = [ln(P/E)+(r+0, 5* d1 = [ln(25/20)+(0, 05+0, 5*0, 045)*0, 5]/(0, 3 √ 0, 5), d1 = [0, 22314+0, 095*0, 5]/0, 2121 d1 = 1, 276. d2 = d1 - d2 = 1, 276 – 0, 3 * √ 0, 5 d2 = 1, 064. Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0, 899, N(d2).= 0, 8563. Шаг 3 Рассчитываем стоимость опциона CALL = P* N(d1) – E*e-rt * N(d2) CALL = 25* 0, 899 – 20*e-0, 05*0, 5 * 0, 8563 = 5, 77. Пример 2. 4 октября 200 г. цена закрытия опциона компании Х со сроком исполнения 21 апреля 2001 г. и ценой исполнения $49 составила $4. Базовые акции продаются по цене $50. 4 октября срок до исполнения составляет 199 дней. Непрерывно начисляемая безрисковая ставка равна 7%. Дисперсия доходности акций составляет 0, 09. Шаг 1.. Рассчитываем значения величин d1 и d2. d1 = [ln(P/E)+(r+0, 5* d1 = [ln(50/49)+(0, 07+0, 5*0, 09)*199/365]/(√ 0, 09*199/365) = 0, 3742 d2 = d1 - d2 = 0, 3742 - √ 0, 09*199/365 = 0, 1527. Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0, 6459 и N(d2) = 0, 5607 Шаг 3 Рассчитываем стоимость опциона CALL = P* N(d1) – E*e-rt * N(d2) CALL = 50* 0, 6459 – 49*e-0, 07*199/365 * 0, 5607= 5, 85. Таким образом, цена опциона, полученная с помощью модели Блэка-Шоулза оказалась выше, чем цена на рынке. Это означает, что опцион недооценен и для инвестора целесообразно приобретение данного опциона. Тесты по дисциплине:
|

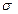 2)*t]/(
2)*t]/(


