БІЛЕТ № 12
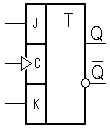
№1 JK - триггер не имеет состояния неопределенности или запрещенной комбинации входных сигналов. Характеризуется следующей таблицей истинности:
-Q-n - меняет состояние выхода на противоположное. Также как RS - триггер, JK - тригер может быть как асинхронным, так и синхронизируемым уровнем или фронтом, однако на практике используют синхронизируемые фронтом.
Согласно таблице состояний синхронный JK- тригер может выполнять функции D - триггера, если исключить комбинации переменных при которых J=K. Это достигается соединением входов J и K через инвертор:
№2 Двійко́ во-десятко́ вий код (ДДК, англ. BCD, binary-coded decimal) —- спосіб представлення десяткового числа, у якому кожній цифрі відповідає певна послідовність двійкових розрядів. Цей код (а точніше, його різновид 8421-ДДК) спрощує ввід/вивід числа у десятковому вигляді, використовується у калькуляторах та при роботі над числами з фіксованою крапкою (наприклад, з грішми) для забезпечення належної точності підрахунків. Реалізація BCD-арифметики досить проста, тому вона присутня у наборах інструкцій майже всіх мікропроцесорів та мікроконтролерів.
Найпростішим варіантом є 8421-ДДК, який означає, що кожна цифра десяткового числа записується своїм двійковим представленням з доповненням нулями до 4 розрядів (тетрада). Наприклад, число 309110, при кодуванні у 8421-ДДК буде виглядати як 0011 0000 1001 0001 2 2 АРИФМЕТИЧНІ ОПЕРАЦІЇ З ДВІЙКОВИМИ ЧИСЛАМИ 2.1 Виконання операції додавання (віднімання) в двійковій системі Подібно до того як із десятковими, так і з двійковими числами можна виконувати всі арифметичні дії. В принципі комп& rsquo; ютер уміє тільки додавати. Всі інші арифметичні дії зводяться до арифметичної операції додавання, логічних операцій зсуву при множенні і діленні. Віднімання заміняється додаванням в додатковому чи зворотньому коді. З метою спрощення виконання арифметичних операцій використовують спеціальні коди для представлення чисел в комп& rsquo; ютері. Саме використання кодів дозволяє звести операцію віднімання чисел до арифметичного додавання кодів цих чисел. Використовуються прямий, зворотній і додатковий коди чисел. Прямий код використовується для представлення додатніх і від& rsquo; мних чисел в запам& rsquo; ятовуючому пристрої комп& rsquo; ютера. Зворотній і додатковий коди використовуються для заміни операції віднімання операцією додавання, що спрощує структуру арифметичного блоку ЕОМ. Додавання в будь-якій р-ковій системі числення виконується порозрядно аналогічно додаванню десяткових чисел на основі таблиці додавання 2.1. Якщо результат додавання двох цифр в даному розряді р-ковій системі числення більше, ніж р-1, то відбувається перенос одиниці в старший розряд. Таблиця 2.1 & ndash; Правила додавання в двійковій системі числення Двійкове додавання 0+0=1 1+0=1 0+1=1 1+1=10 Віднімання в р-ковій системі числення також виконується попрозрядно стовбчиком по аналогії з десятковою системою числення за допомогою таблиці& nbsp;.2. Якщо в даному розряді зменшуване число менше від& rsquo; ємника, то позичається одиниця зі старшого розряду. В двійковій системі числення позичина одиниця зі старшого розряду дорівнює двом одиницям даного розряду. Таблиця 2.2 & ndash; Правила віднімання в двійковій системі числення Двійкове віднімання 0 & ndash; 0=0 1 & ndash; 0=1 1 & ndash; 1=0 10 & ndash; 1=1 Множення двох багатозначних чисел в р-ковій системі числення також виконується за тими ж правилами, що і в десятковій системі з послідовним множенням цифр першого множника на другий множник з допомогою таблиці& nbsp;.3. Таблиця 2.3 & ndash; Правила множення в двійковій системі числення Двійкове множення 0 0=0 1 0=0 0 1=0 1 1=1 При діленні стовбчиком в р-ковій системі числення виконуються дії множення і віднімання. Ділення двійкових чисел зводиться до порівняння цих чисел між собою і віднімання з більшого числа меншого. Якщо результата ділення не є кінцевим р-ковим дробом, то необхідно виділити неперіодичну частину дробу і її період. Залежно від способу обробки бітів, розміщених у розрядній сітці, розрізняють два види кодів: паралельний, коли в кожний момент часу всі розряди сітки доступні для обробки, і послідовний, коли в кожний момент часу доступний один розряд сітки. Числа, подані паралельним кодом, доступні за один такт, а числа, подані послідовним кодом, - за n тактів, де n - розрядність сітки. Якщо розрядність числа перевищує довжину сітки, то його обробка ведеться частинами. Натуральним кодом називають подання числа як цілого беззнакового у двійковій системі числення. Діапазон подання чисел у натуральному коді для n- розрядної сітки становить від 0 до 2n-1, тобто для 8-розрядної сітки - від 0 до 255. Для подання цілих знакових чисел використовують прямий, обернений і додатковий коди. Старший розряд сітки є знаковим. Значення цього розряду дорівнює 0 для додатних чисел і 1 - для від'ємних. В інших розрядах розміщується модуль числа. Якщо до натурального коду цілого числа додати знаковий розряд, одержуємо запис числа у прямому коді. Домовимося знаковий розряд розташовувати зліва і відокремлювати від розрядів модуля числа крапкою. Використання ПК забезпечує виконання операції додавання двох додатніх чисел звичайним способом без будь-яких складностей - не варто лише робити перенос одиниці старшого розряду модуля суми у знаковий розряд. Тобто при виконанні арифметичних операцій над прямим кодом двійкових чисел знаковий розряд і розряди модуля не можна розглядати як єдине ціле. Іншою формою запису двійкових чисел є обернений код. Обернений код двійкового від'ємного числа утворюється з прямим кодом рівного йому за модулем додатнього числа шляхом інвертування значень усіх його розрядів. Або: обернений код від'ємного числа утворюється шляхом інверсії всіх розрядів модуля цього числа, записаного у прямому коді. Знаковий розряд при цьому зберігає значення 1. При виконанні арифметичних операцій над двійковими числами, поданими в обернений код, знаковий розряд і розряд модуля числа можна розглядати як єдине ціле (перенос одиниці зі старшого розряду модуля суми в знаковий розряд не приводить до помилкового результату), але нуль як і раніше має два зображення - «додатнє» і «від'ємне». Слід зазначити, що отриманий при додаванні від'ємний результат також утворюється в обернений код. У цьому випадку число може бути перетворене у прямому коді інверсією всіх значущих розрядів (розрядів модуля). Найбільше поширення в обчислювальних пристроях одержало подання від'ємних двійкових чисел за допомогою додаткового коду. ДК від'ємного числа утворюється з його прямого коду за правилом: - у знаковому розряді залишається одиниця; - розряди модуля числа інвертуються; - до молодшого розряду додається одиниця. Очевидно, що додатковий код від'ємного числа утворюється з його оберненого коду додаванням одиниці до молодшого розряду. Операція одержання додаткового коду від'ємного числа з прямого коду рівного йому за модулем додатнього числа називається операцією доповнення. Ця операція полягає в інвертуванні всіх розрядів вихідного коду (включаючи знаковий) і додавання до молодшого розряду одиниці. Таким чином, сформулюємо наступне правило: у системі двійкових чисел із знаком заміна додатнього числа на рівне йому за модулем від'ємне і навпаки, від'ємного на додатнє, здійснюється шляхом застосуванням до коду даного числа операції доповнення. Ця властивість подання від'ємних чисел у двійковому коді дозволяє при виконанні арифметичних операцій взагалі відмовитися від операції віднімання, замінивши її операцією додавання з числом, що має знак, протилежний знаку числа, яке віднімається. 2.2 Десяткові числа в упакованому і неупакованому форматах Сьогодні найбільш поширеними є два формати представлення десяткових чисел в мікропроцесорах & ndash; упакований двійково-десятковий код (BCD-Binary-Coded Decimal) і неупакований десятковий код. Упакований BCD-код & ndash; це таке представлення десяткового числа, при якому кожна десяткова цифра представляється 4-х бітним двійковим позиційним кодом 8-4-2-1. При цьому байт складається з двох десяткових цифр. Молодша десяткова цифра займає праву тетраду (біти 3: 0), старша & ndash; ліву тетраду (біти 7: 4). Багаторозрядні BCD-числа займають декілька суміжних байт. Якщо число є знаковим, то для представлення знака в BCD-форматі відводиться старша тетрада старшого байта. Для кодування знака можна використовувати 6 двійкових кодових комбінацій, котрі не використовуються для представлення десяткових цифр. Це коди 1010-1111 (A-F в шістнадцятковому представлені). Зазвичай для кодування знака “плюс” використовують код 1100 (C), а для знака “мінус” & ndash; 1101 (D). Неупакований десятковий код є підмножиною міжнародної таблиці кодування символів ASCII (таблиця 1.1). Очевидно, для зберігання неупакованих десяткових чисел необхідно вдвічі більше пам& rsquo; яті, оскільки кожна цифра представляється 8-бітовим кодом. №3 Текст програми на мові асемблера записується в один або кілька файлів, імена файлів і їх розширення можуть бути будь-які, прийнято для файлів які містять програми мовою асемблера прийнято використовувати розширення *.asm. Для файлів визначених констант і повних типів розширення *.inc. Ці файли є текстовими їх можна набрати в будь-якому текстовому редакторі. Можна також використати інтегровані середовища для розробки програм, при програмуванні зручно виділяти один каталог для збереження всіх файлів програми і звідти запускати всі необхідні програми для підготовки, асемблювання та компонування програми. При використанні стандартних редакторів тексту, редаговані тексти треба зберігати у вигляді звичайних файлів у форматі ASCII, це означає, що ці файли треба зберігати без додаткових символів, ці символи часто вставляють в текст різні спеціалізовані редактори, наприклад WORD. Асемблювання програми. Підготовлений текст мови асемблер є початковим для спеціальних програм, які називаються асемблерами, далі програма асемблера. Задача програми асемблера перетворити текст програми у форму двійкових команд, останні можуть вже бути виконанні мікропроцесором. Після асемблювання дістають так звані файли об'єктних модулів, які мають відповідні розширення *.obj. Для отримання об'єктних файлів необхідного виконати відповідну програму асемблера masm фірми Microsoft, або tasm фірми Borland. В обох випадках після команди вказується ім'я файлу: masm prog1.asm, tasm prog1.asm. Така форма команди є мінімальною, крім цієї форми можна використовувати іншу форму задаючи перед іменем файлу опції або ключі. Якщо програма складається з декількох файлів, то їх асемблювання проводиться незалежно один від одного, хоча отримані об'єктні файли представлені вже в двійковій формі запускати їх на виконання не можливо. Компоновка програми. Текст програми може знаходитись в декількох файлах, змінні які описані в цих файлах можуть використовуватися спільно, якщо такі файли асемблюються окремо, то не можливо дістати повну інформацію, для того, щоб генерувати виконавчий код. Тому процес підготовки програми обов'язково включає в себе етап компоновки. На цьому етапі визначають всі невідомі, при окремому асемблювані, адреси всіх змінних або функцій, які використовуються спільно. Процес об'єднання об'єктних модулів в один файл виконується спец. програмою, яка називається компоновщиком. Це може бути програма link фірми Microsoft, або tlink фірми Borland, отримуваний виконуваний файл має розширення *.exe, або *.com. Компановщику треба передати імена відповідних об'єктних файлів. Link prog1.obj prog2.obj Tlink prog1.obj prog2.obj Після компонування отримується виконуваний файл, він отримує ім'я файла, який стоїть перший у відповідній команді.Відладка програми. За винятком початкових простих програм практично всі програми на мові асемблера мають потребу в відладці. Для відладки можна використовувати різні відладчики, наприклад tg386-Turbo Debuger фірми Borland. Сучасні відладчики дозволяють в процесі відладки контролювати значення регістрів загального призначення, а також значення змінних і змінювати їх в процесі відладки, можна переглядати зміст різних ділянок пам'яті, можна контролювати виконання покроково, або розставляти точки зупинки.Використання інтегрованих середовищ (ІС).
|