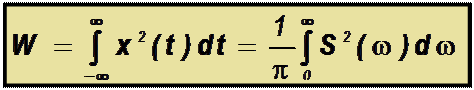Найдём энергию непериодических сигналов, умножив на t, т.е. отбросив в формуле множитель 1/t
Рассмотрим в общем случае сигнал на бесконечном интервале времени:
Интегралы сходятся, поэтому можно изменить порядок интегрирования
Принимается во внимание, что внутренний интеграл – комплексно сопряженная функция спектральной плотности). С учётом чётности подинтегрального выражения окончательно получим
Из этого выражения, называемого равенством Парсеваля следует, что энергия сигнала складывается из бесконечно большого числа слагаемых, представляющих
Энергию составляющих спектра на бесконечно малой полосе dw вблизи соответствующих мгновенных частот w. Величина характеризует распределение энергии по спектру и называется энергетической спектральной плотностью.
|


 .
.