Комплексные спектры единичных скачков в соответствии с теоремой о запаздывании
Другой вариант расчёта спектра прямоугольного импульса
S( j w ) = и совпадает со своим модулем: | S( j w ) | = S( w ) = 1. Спектр амплитуд - сплошной, простирающийся до бесконечно больших значений -w и +w с неизменной спектральной плотностью при всех частотах, равной 1. Если бесконечный спектр d-сигнала ограничить частотой среза wс (как показано на рис.), то единичный импульс принимает вид сигнала, описываемого функцией вида sin w сt/ w сt. Её называют во многих литературных источниках функцией отсчётов и обозначают Sa( a ). Такая функция равна 1 при a=0 (при нулевом аргументе), а с увеличением a изменяется по закону затухающего синуса Другой вариант – расчёт спектра одиночного прямоугольного импульса с длительностью t и площадью, равной 1.
|
, а спектр амплитуд неизменен 
Спектр единичного скачка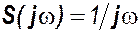 
. Согласно теореме о запаздывании сигнала спектры сигналов х1 и х2 будут
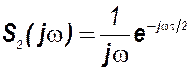
Тогда на основании теорем о сумме спектров и о смещении сигнала спектр прямоугольного импульса находится как разность спектров неединичных скачков:
Комплексный спектр единичного импульса
(t) e-j w tdt = 
(t)e-j w tdt = e-j w 0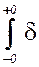 
(t) dt = 1,
