
 Отримання зображень розподілу речовини по перерізах непрозорого об’єкту без його руйнування уможливилося після відкриття явищ радіоактивних (А.А. Беккерель, 1896 р) та Х- (В.К. Рентґен, 1895 р) променів, здатних проникати крізь непрозорі тіла (з поглинанням у внутрішньому середовищі цих тіл). Причому І.П. Пулюєм Х- променеві тіньові зображення на фотопластинках було отримано та опубліковано майже за сім років до отримання пріоритету В.К. Рентґеном на відкриття Х- променів. З самого початку ХХ-го ст. дістали широке поширення апарати для рентгенографії та дещо пізніше — радіографії. Були розроблені та побудовані (30-40 рр. ХХ ст.) й апарати для пошарової та одночасно багатошарової (симультанної, simultaneously — одночасно, англ.) томографії (стратиграфії, strata — шар, лат.), рис. 3.1 [1]. В їх основу евристично (правдоподібно) покладено принципи оптомеханіки та проективної геометрії (рис. 2.1, розділ 2).
Отримання зображень розподілу речовини по перерізах непрозорого об’єкту без його руйнування уможливилося після відкриття явищ радіоактивних (А.А. Беккерель, 1896 р) та Х- (В.К. Рентґен, 1895 р) променів, здатних проникати крізь непрозорі тіла (з поглинанням у внутрішньому середовищі цих тіл). Причому І.П. Пулюєм Х- променеві тіньові зображення на фотопластинках було отримано та опубліковано майже за сім років до отримання пріоритету В.К. Рентґеном на відкриття Х- променів. З самого початку ХХ-го ст. дістали широке поширення апарати для рентгенографії та дещо пізніше — радіографії. Були розроблені та побудовані (30-40 рр. ХХ ст.) й апарати для пошарової та одночасно багатошарової (симультанної, simultaneously — одночасно, англ.) томографії (стратиграфії, strata — шар, лат.), рис. 3.1 [1]. В їх основу евристично (правдоподібно) покладено принципи оптомеханіки та проективної геометрії (рис. 2.1, розділ 2).
У 1917 р. Й. Радоном було створено теоретичні основи для розроблення методів побудови зображень перерізу тіла за їх проекціями по многовиду ліній [2]. Лише у 1953 р. офіційно зауважено фундаментальну роль цієї праці для томографії (її виклав проф. Й. Влока у своїй лекції „Зображення поперечних січень” у відповідь на запитання доктора медицини Маєрека [3, 4]).
При розв’язуванні задач математичної фізики, до якої належить й задача томографії, часто використовують відображення функцій дійсного аргументу (наприклад, які є моделями змін фізичних величин у часові) до функцій комплексного аргументу, який інтерпретується через частоту. За відповідних умов, що накладаються на функції, таке відображення є взаємнооднозначним (або — ізоморфізмом, рис.3.2). При цьому й самі задачі дістають представлення в іншій області — частотній, застосування якого спрощується розв’язання задачі.
Найвідомішим відображенням в частотну область є перетворення Фур’є функцій від часу у функції від комплексної частоти. При застосуванні перетворення Фур’є до радонівського образу
 , (3. 1)
, (3. 1)
 Рис. 3.2
Рис. 3.2
|
функції 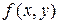 , аргументи
, аргументи  якої є просторовими координатами, зміст поняття частоти (розмірність якої 1/сек) міняється. Аргументом функції-образу стає " просторова частота" (її розмірність 1/м). Перетворення Фур’є уможливлює розв’язок задачі визначення функції
якої є просторовими координатами, зміст поняття частоти (розмірність якої 1/сек) міняється. Аргументом функції-образу стає " просторова частота" (її розмірність 1/м). Перетворення Фур’є уможливлює розв’язок задачі визначення функції 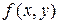 при відомому радонівському образі
при відомому радонівському образі  обчислювальним, а не аналоговим методом. При цьому необхідно забезпечити виконання потрібних властивостей функцій —
обчислювальним, а не аналоговим методом. При цьому необхідно забезпечити виконання потрібних властивостей функцій — 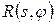 та
та  для існування їх Фур’є – образів
для існування їх Фур’є – образів  та
та  .
.
Якщо  — одновимірне перетворення Фур'є функції
— одновимірне перетворення Фур'є функції 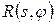 за змінною s, а
за змінною s, а  — двовимірне перетворення Фур'є функції
— двовимірне перетворення Фур'є функції  за змінними x та y, тоді, за означенням Фур’є перетворення
за змінними x та y, тоді, за означенням Фур’є перетворення
 , (3. 2)
, (3. 2)
 , (3. 3)
, (3. 3)
де
 (3. 4)
(3. 4)
справедливим є твердження (теорема про центральний переріз) [5]:
Якщо для функції  існує її радонівський образ
існує її радонівський образ 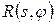 , а також їх Фур’є – образи
, а також їх Фур’є – образи  та
та  , то спектр функції за змінною
, то спектр функції за змінною 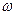 описує переріз двовимірного спектру при фіксованому
описує переріз двовимірного спектру при фіксованому 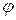 , тобто
, тобто
 . (3. 5)
. (3. 5)
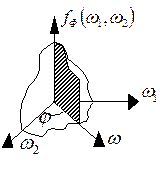 Рис. 3.3
Рис. 3.3
|

 На рис. 3.3 наведено геометричну інтерпретацію кута
На рис. 3.3 наведено геометричну інтерпретацію кута 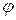 з радонівського образу в кут
з радонівського образу в кут 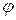 перерізу двовимірного спектру
перерізу двовимірного спектру  функції-розподілу речовини. Формула (3.5) однозначно пов’язує спектри радонівського образу та томоґрафічного зображення і уможливлює визначення другого за першим. Отже, для розв’язання основної задачі томоґрафії потрібно знайти спектри радонівських образів за змінною s для всіх значень
функції-розподілу речовини. Формула (3.5) однозначно пов’язує спектри радонівського образу та томоґрафічного зображення і уможливлює визначення другого за першим. Отже, для розв’язання основної задачі томоґрафії потрібно знайти спектри радонівських образів за змінною s для всіх значень 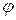 і вони будуть відображати всі перерізи Фур’є-образу
і вони будуть відображати всі перерізи Фур’є-образу  шуканої функції
шуканої функції  . Тобто існує можливість здійснити низку перетворень:
. Тобто існує можливість здійснити низку перетворень: 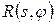 ®
®  ®
®  ®
®  . Фактично рівнянням (3.5) в області просторових частот замінюється рівняння (3.1) в області лінійних розмірів. Для ідеального випадку, коли відомі значення радонівського образу для всіх кутів
. Фактично рівнянням (3.5) в області просторових частот замінюється рівняння (3.1) в області лінійних розмірів. Для ідеального випадку, коли відомі значення радонівського образу для всіх кутів  теорема про центральний переріз дає можливість знайти спектр томоґрафічного зображення для всіх значень частот
теорема про центральний переріз дає можливість знайти спектр томоґрафічного зображення для всіх значень частот  , тобто однозначно відновити
, тобто однозначно відновити  . На рис. 3.4 наведено операторну схему теореми [6] (в квадратних дужках наведено обчислювальну складність оператора[10], де n — кількість відліків функції для оператора її перетворення; функцію розподілу густини
. На рис. 3.4 наведено операторну схему теореми [6] (в квадратних дужках наведено обчислювальну складність оператора[10], де n — кількість відліків функції для оператора її перетворення; функцію розподілу густини  позначено через
позначено через  , інші позначення відповідають контексту теореми.
, інші позначення відповідають контексту теореми.  На практиці виникають проблеми, пов’язані з тим, що радонівський образ відомий лише для скінченної кількості дискретних кутів, а проекційні дані отримані з певною похибкою для дискретних значень параметра s. Тому методи відновлення повинні враховувати відмінності між теоретичною та практичною частинами відбору та представлення даних томографії.
На практиці виникають проблеми, пов’язані з тим, що радонівський образ відомий лише для скінченної кількості дискретних кутів, а проекційні дані отримані з певною похибкою для дискретних значень параметра s. Тому методи відновлення повинні враховувати відмінності між теоретичною та практичною частинами відбору та представлення даних томографії.
Теорема про центральний переріз є частинним випадком загальнішої, проективної теореми, у якій Фур’є перетворення замінено проективним перетворенням:
 , (3. 6)
, (3. 6)
де ядро  проективного перетворення може набирати різного вигляду:
проективного перетворення може набирати різного вигляду:
a)  — як в теоремі про центральний переріз;
— як в теоремі про центральний переріз;
b)  , тоді для кола радіусом a маємо:
, тоді для кола радіусом a маємо:  ;
;
c)  — результатом такого перетворення будуть моментні функції m - го порядку;
— результатом такого перетворення будуть моментні функції m - го порядку;
d)  .
.
Таким чином, при побудові алґоритмів реконструкції для конкретних томоґрафів можуть використовуватись інші ядра (не тільки ядро Фур’є перетворення). Ядро вибирається (наприклад, простим підбором) залежно від типу многовиду ліній L. Останній визначається фізикою процесу поширення потоків частинок, хвиль тощо у томографі та методом сканування. Крім цього потрібно враховувати деякі додаткові вимоги. Зокрема, для множини паралельних ліній (наприклад, колімовані Х-промені, collimare, лат.) та однорідних, ізотропних середовищ оптимальним (за критерієм мала обчислювальна складність[11] при заданих параметрах і точності томографічного зображення) є ядро (а).


 Отримання зображень розподілу речовини по перерізах непрозорого об’єкту без його руйнування уможливилося після відкриття явищ радіоактивних (А.А. Беккерель, 1896 р) та Х- (В.К. Рентґен, 1895 р) променів, здатних проникати крізь непрозорі тіла (з поглинанням у внутрішньому середовищі цих тіл). Причому І.П. Пулюєм Х- променеві тіньові зображення на фотопластинках було отримано та опубліковано майже за сім років до отримання пріоритету В.К. Рентґеном на відкриття Х- променів. З самого початку ХХ-го ст. дістали широке поширення апарати для рентгенографії та дещо пізніше — радіографії. Були розроблені та побудовані (30-40 рр. ХХ ст.) й апарати для пошарової та одночасно багатошарової (симультанної, simultaneously — одночасно, англ.) томографії (стратиграфії, strata — шар, лат.), рис. 3.1 [1]. В їх основу евристично (правдоподібно) покладено принципи оптомеханіки та проективної геометрії (рис. 2.1, розділ 2).
Отримання зображень розподілу речовини по перерізах непрозорого об’єкту без його руйнування уможливилося після відкриття явищ радіоактивних (А.А. Беккерель, 1896 р) та Х- (В.К. Рентґен, 1895 р) променів, здатних проникати крізь непрозорі тіла (з поглинанням у внутрішньому середовищі цих тіл). Причому І.П. Пулюєм Х- променеві тіньові зображення на фотопластинках було отримано та опубліковано майже за сім років до отримання пріоритету В.К. Рентґеном на відкриття Х- променів. З самого початку ХХ-го ст. дістали широке поширення апарати для рентгенографії та дещо пізніше — радіографії. Були розроблені та побудовані (30-40 рр. ХХ ст.) й апарати для пошарової та одночасно багатошарової (симультанної, simultaneously — одночасно, англ.) томографії (стратиграфії, strata — шар, лат.), рис. 3.1 [1]. В їх основу евристично (правдоподібно) покладено принципи оптомеханіки та проективної геометрії (рис. 2.1, розділ 2). , (3. 1)
, (3. 1) Рис. 3.2
Рис. 3.2
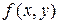 , аргументи
, аргументи  якої є просторовими координатами, зміст поняття частоти (розмірність якої 1/сек) міняється. Аргументом функції-образу стає " просторова частота" (її розмірність 1/м). Перетворення Фур’є уможливлює розв’язок задачі визначення функції
якої є просторовими координатами, зміст поняття частоти (розмірність якої 1/сек) міняється. Аргументом функції-образу стає " просторова частота" (її розмірність 1/м). Перетворення Фур’є уможливлює розв’язок задачі визначення функції  обчислювальним, а не аналоговим методом. При цьому необхідно забезпечити виконання потрібних властивостей функцій —
обчислювальним, а не аналоговим методом. При цьому необхідно забезпечити виконання потрібних властивостей функцій — 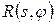 та
та  для існування їх Фур’є – образів
для існування їх Фур’є – образів  та
та  .
. , (3. 2)
, (3. 2) , (3. 3)
, (3. 3) (3. 4)
(3. 4)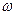 описує переріз двовимірного спектру при фіксованому
описує переріз двовимірного спектру при фіксованому 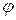 , тобто
, тобто . (3. 5)
. (3. 5)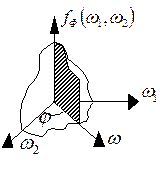 Рис. 3.3
Рис. 3.3

 На рис. 3.3 наведено геометричну інтерпретацію кута
На рис. 3.3 наведено геометричну інтерпретацію кута  ®
®  теорема про центральний переріз дає можливість знайти спектр томоґрафічного зображення для всіх значень частот
теорема про центральний переріз дає можливість знайти спектр томоґрафічного зображення для всіх значень частот  , тобто однозначно відновити
, тобто однозначно відновити  , інші позначення відповідають контексту теореми.
, інші позначення відповідають контексту теореми.  На практиці виникають проблеми, пов’язані з тим, що радонівський образ відомий лише для скінченної кількості дискретних кутів, а проекційні дані отримані з певною похибкою для дискретних значень параметра s. Тому методи відновлення повинні враховувати відмінності між теоретичною та практичною частинами відбору та представлення даних томографії.
На практиці виникають проблеми, пов’язані з тим, що радонівський образ відомий лише для скінченної кількості дискретних кутів, а проекційні дані отримані з певною похибкою для дискретних значень параметра s. Тому методи відновлення повинні враховувати відмінності між теоретичною та практичною частинами відбору та представлення даних томографії. , (3. 6)
, (3. 6) проективного перетворення може набирати різного вигляду:
проективного перетворення може набирати різного вигляду: — як в теоремі про центральний переріз;
— як в теоремі про центральний переріз; , тоді для кола радіусом a маємо:
, тоді для кола радіусом a маємо:  ;
; — результатом такого перетворення будуть моментні функції m - го порядку;
— результатом такого перетворення будуть моментні функції m - го порядку; .
.


