Зворотнє проектування
Оскільки первинною процедурою томографії є експериментальне визначення радонівського образу зображення перерізу об’єкту (проектування цього перерізу) то логічно поставити задачу побудови самого зображення перерізу за його проекцією, тобто — виконання зворотнього проектування. Для побудови методу зворотнього проектування проаналізуймо спочатку двовимірну функцію
Співвідношення (4.1) є виразом правила, за яким функції однієї змінної Побудуймо вираз, у якому враховано те, що для кожного кута
яка на відміну від функції Оскільки радонівський образ
Переріз площиною За аналоґією з (4.2) означується сумарна зворотня проекція
(сумарне зображення). Сумарна проекція є функцією двох ґеометричних координат x та y і містить проекційні дані для всіх кутів
Підставивши (4.5) в (4.4), отримаємо
і, для меж інтеґрування
Подамо сумарну проекцію через двовимірне обернене перетворення Фур’є її спектру в декартовій і полярній системі координат:
Порівнявши (4.7) і (4.8), бачимо, що для
або, в координатах
Це означає, що за Фур’є образом сумарної проекції отримано Фур’є образ томоґрафічного зображення. Вираз
є модулем характеристики передачі фільтра, а
є імпульсною характеристикою цього фільтра (як обернене Фур’є-перетворення від частотної характеристики). Тоді зображення визначається за згорткою сумарної проекції з імпульсною характеристикою фільтра:
Формула (4.13) використовується для реконструкції методом r -фільтрації[13].
|

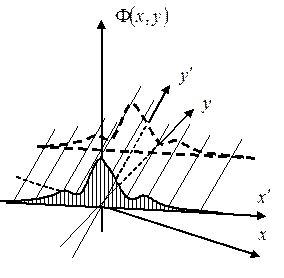 Рис. 4.1
Рис. 4.1
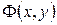 , значенння якої при переміщенні вздовж будь-якої прямої, паралельної до осі
, значенння якої при переміщенні вздовж будь-якої прямої, паралельної до осі 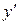 , не змінюються, рис.4.1 [1]. Значення функції
, не змінюються, рис.4.1 [1]. Значення функції  від однієї з цих паралельних прямих до іншої. Тоді ці значення є деякою функцією
від однієї з цих паралельних прямих до іншої. Тоді ці значення є деякою функцією  однієї змінної s (на осі
однієї змінної s (на осі 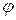 , то з рівності
, то з рівності 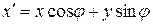 маємо:
маємо: . (4. 1)
. (4. 1)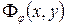 для кожного кута
для кожного кута 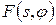 . Якщо підсумувати з усередненням в кожній точці (x, y) значення цих “розтягнутих” функцій, то при нескінченно малому зменшенні інтервалів між точками отримаємо нову функцію
. Якщо підсумувати з усередненням в кожній точці (x, y) значення цих “розтягнутих” функцій, то при нескінченно малому зменшенні інтервалів між точками отримаємо нову функцію , (4. 2)
, (4. 2)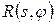 , отриманий під даним кутом
, отриманий під даним кутом 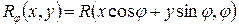 . (4. 3)
. (4. 3)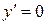 цієї функції описується функцією
цієї функції описується функцією 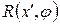 . Функцію
. Функцію 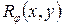 називають зворотньою проекцією. Така проекція містить дані лише для одного кута
називають зворотньою проекцією. Така проекція містить дані лише для одного кута  , (4. 4)
, (4. 4) . Для побудови залежності між
. Для побудови залежності між 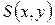 та
та 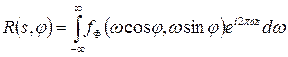 . (4. 5)
. (4. 5) , (4. 6)
, (4. 6)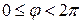 ,
, 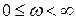 , отримаємо:
, отримаємо: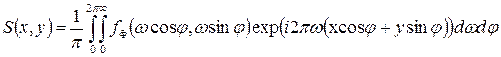 . (4. 7)
. (4. 7)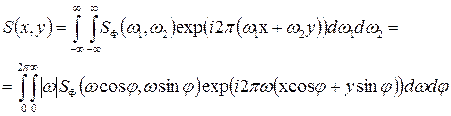 . (4. 8)
. (4. 8)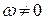 ,
,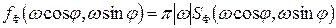 , (4. 9)
, (4. 9) ,
,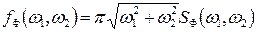 . (4. 10)
. (4. 10)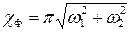 (4. 11)
(4. 11)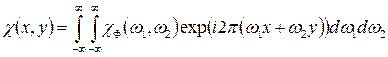 (4. 12)
(4. 12) . (4. 13)
. (4. 13)


