Метод реконструкції на основі зворотнього проектування
Тотожними перетвореннями результатів, які витікають з теореми про центральне січення, отримується вираз зворотного проектування, але одновимірною згорткою. Визначимо зображення
В полярній системі координат, коли
Підставивши
Підставмо вираз (3.2) у (4.16) і отримаймо формулу реконструкції
Звідси, зміною порядку інтеґрування по s i , отримаємо, що
де
є імпульсною характеристикою фільтра з модулем функції передачі (частотною характеристикою) Формула (4.17) уможливлює реконструювання зображення за допомогою зворотнього проектування вже профільтрованих проекцій, чим усувається потреба у двовимірній згортці (4.13), що зменшує кількість обчислювальних та часових ресурсів. Згортка і зворотнє проектування за формулою (4.18) виконується такою послідовністю операцій:
1) виконується одновимірна згортка по s проекцій
2) виконується зворотнє проектування за формулою
Наведені методи реконструкції побудовані на основі методів, яківипливають з інтеґральних перетворень [2] (Фур’є та Радона). Причому, задача реконструкції ставилася та розв’язувалася в неперервному випадку. На практиці отримані формули замінюються їх дискретними аналогами. Проте, отримані методи є математично коректними для ідеального випадку (коли взаємодія зондуючого випромінювання з речовиною біооб’єкта відбувається за лінійним законом, радонівський образ неперервно залежить від кута та параметра s, дані отримуються без похибки тощо) [3, 4]. В практичних задачах кожний з методів має свої недоліки та переваги з точки зору зручності реалізації, швидкодії, точності, стійкості, відсутності артефактів, можливості врахування додаткової апріорної інформації і т. д. Тому при проектуванні конкретних томоґрафів специфіка біооб’єктів, конструкцій скануючої системи, параметрів випромінювання та, навіть, наявної елементної бази для реалізації обчислювальних пристроїв впливає на вибір того чи іншого алгоритму з низки відомих, або спричиняє необхідність удосконалення їх чи синтезу нових. Наприклад, існують методи реконструкції (з розкладом в скінченні ряди, ітераційні), в яких задача зразу формулюється у дискретній формі, і розв’язання її фактично зводиться до розв’язання систем рівнянь [5].
|

 в просторовій області за його двовимірним спектром
в просторовій області за його двовимірним спектром  шляхом його оберненого перетворення Фур’є:
шляхом його оберненого перетворення Фур’є: . (4. 14)
. (4. 14) , (4.14) набирає вигляду:
, (4.14) набирає вигляду: . (4. 15)
. (4. 15) з формули (3.5) і врахувавши симетрію
з формули (3.5) і врахувавши симетрію  , з (4.15) отримаємо:
, з (4.15) отримаємо: . (4. 16)
. (4. 16)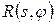 :
: . (4. 17)
. (4. 17) , (4. 18)
, (4. 18) (4. 19)
(4. 19) .
. для кожного з кутів
для кожного з кутів 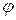 за формулою
за формулою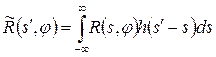 ; (4. 20)
; (4. 20)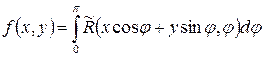 . (4. 21)
. (4. 21)


