Конкретний вираз оператора T задається в основному типом випромінювання, що використовується в томоґрафії. В ідеальному випадку цей оператор повинен бути інтеґральним оператором Радона:  , тобто, щоб виміряні значення p були рівними значенням інтеґралів від функції розподілу речовини всередині об’єкту дослідження по многовиду (прямих). Найближче від такої ідеальної моделі лежить Х-променева томоґрафія, бо Х- фотони (або, як їх ще називають, рентгенівські гама-кванти), якщо знехтувати їх розсіянням на ядрах молекул досліджуваної речовини, вторинними ефектами поширюються прямолінійно. Крім того, ступінь поглинання фотонів при проходження через речовину є інтеґральною характеристикою від лінійного коефіцієнта поглинання Х-променів. Побудувавши відповідну вимірювальну систему, можна добитись досить точної відповідності операторів T та R. Це стало однією з причин побудови історично першим Х- променевого томографа, хоч дослідження проводилися спочатку над радіоактивними випромінюваннями.
, тобто, щоб виміряні значення p були рівними значенням інтеґралів від функції розподілу речовини всередині об’єкту дослідження по многовиду (прямих). Найближче від такої ідеальної моделі лежить Х-променева томоґрафія, бо Х- фотони (або, як їх ще називають, рентгенівські гама-кванти), якщо знехтувати їх розсіянням на ядрах молекул досліджуваної речовини, вторинними ефектами поширюються прямолінійно. Крім того, ступінь поглинання фотонів при проходження через речовину є інтеґральною характеристикою від лінійного коефіцієнта поглинання Х-променів. Побудувавши відповідну вимірювальну систему, можна добитись досить точної відповідності операторів T та R. Це стало однією з причин побудови історично першим Х- променевого томографа, хоч дослідження проводилися спочатку над радіоактивними випромінюваннями.
Взаємодія Х–випромінювання з речовиною найповніше описується рівнянням переносу (Больцмана) [1]:
 , (5.6)
, (5.6)
де  — векторний диференціальний оператор, r — просторові координати, W — кутові координати, Е — енергія частинок (фотонів);
— векторний диференціальний оператор, r — просторові координати, W — кутові координати, Е — енергія частинок (фотонів);  — функція розподілу фотонів по простору r, напрямах W та енергіях Е всередині об’єкту;
— функція розподілу фотонів по простору r, напрямах W та енергіях Е всередині об’єкту;  — функція розподілу фотонів від джерела X-випромінювання; f (r, E) — характеристика середовища;
— функція розподілу фотонів від джерела X-випромінювання; f (r, E) — характеристика середовища;  — макросічення релеївського та комптонівського розсіювання. Потік фотонів розкладається в ряд Наймана
— макросічення релеївського та комптонівського розсіювання. Потік фотонів розкладається в ряд Наймана
 , (5.7)
, (5.7)
де Ip — потік первинних (нерозсіяних) фотонів, In — потік n -кратно розсіяних фотонів.
Для рівняння переносу оператор  та функції
та функції 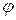 і
і  набирають вигляду:
набирають вигляду:
 ,
,  ,
,  .
.
Рівняння Больцмана є рівнянням у частинних похідних першого порядку, стаціонарне. Крайові і граничні умови визначаються схемою сканування, конструкцією джерел випромінювання, властивостями самого біооб’єкта та його розміщенням відносно скануючої системи.
Енергія X-випромінювання в медичній томоґрафії не перевищує 120 кеВ, основну частину (> 99%) становлять однократно розсіяні фотони [2, 3]. Тому рівняння (5.6) спрощується:
 . (5.8)
. (5.8)
Для томоґрафів з паралельною схемою сканування, з пристроями (коліматорами) для зменшення ширини пучка фотонів та ослаблення ефектів розсіювання та звуження спектру Х-випромінювання і достатньо високими рівнями енергії вираз взаємодії випромінювання з речовиною описується рівнянням:
 , (5.9)
, (5.9)
де c0 > 0 — потужність джерела випромінювання, r 0 — його координати, W — напрям колімації, E 0 — енергія X-фотонів джерела,  .
.
Для двовимірного випадку, розв'язуючи (5.9) відносно  і замінивши
і замінивши  , де
, де  — нормальні координати на площині, отримаємо:
— нормальні координати на площині, отримаємо:
 , (5.10)
, (5.10)
де 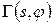 — лінії поширення випромінювання. Як видно з виразу (5.10), кількість зареєстрованих на виході з біооб’єкта фотонів експоненційно залежить від інтеґрального коефіцієнта ослаблення Х-випромінювання вздовж лінії проходження цього випромінювання через біооб’єкт.
— лінії поширення випромінювання. Як видно з виразу (5.10), кількість зареєстрованих на виході з біооб’єкта фотонів експоненційно залежить від інтеґрального коефіцієнта ослаблення Х-випромінювання вздовж лінії проходження цього випромінювання через біооб’єкт.
Приведемо вираз (5.10) до вигляду основного рівняння томоґрафії. Поділимо праву і ліву його частину на c0 і пролоґарифмуємо його. Введемо оператор U, що „переводить”  в радонівський образ
в радонівський образ 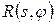 :
:
 , (5.11)
, (5.11)
Отже, отримано лінійну залежність між інтеґральним коефіцієнтом ослабленням Х-випромінювання вздовж лінії його поширення та радонівською проекцією:
 . (5.12)
. (5.12)
Многовид кривих 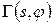 задається схемою сканування. Якщо знехтувати n -кратно розсіяними фотонами, то многовид
задається схемою сканування. Якщо знехтувати n -кратно розсіяними фотонами, то многовид 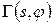 стає наборами паралельних (для випадку схеми сканування з одним детектором), або віялоподібних (для схеми сканування з лінійкою детекторів) ліній. Формула (5.12) є математичним записом перетворення Радона. Задача знаходження оберненого перетворення розв'язана [4, 5].
стає наборами паралельних (для випадку схеми сканування з одним детектором), або віялоподібних (для схеми сканування з лінійкою детекторів) ліній. Формула (5.12) є математичним записом перетворення Радона. Задача знаходження оберненого перетворення розв'язана [4, 5].
Формула (5.10) набирає вигляду [6]:
 , (5.13)
, (5.13)
коли I залежить від Е (спектр пучка фотонів не моноенергетичний).

 , тобто, щоб виміряні значення p були рівними значенням інтеґралів від функції розподілу речовини всередині об’єкту дослідження по многовиду (прямих). Найближче від такої ідеальної моделі лежить Х-променева томоґрафія, бо Х- фотони (або, як їх ще називають, рентгенівські гама-кванти), якщо знехтувати їх розсіянням на ядрах молекул досліджуваної речовини, вторинними ефектами поширюються прямолінійно. Крім того, ступінь поглинання фотонів при проходження через речовину є інтеґральною характеристикою від лінійного коефіцієнта поглинання Х-променів. Побудувавши відповідну вимірювальну систему, можна добитись досить точної відповідності операторів T та R. Це стало однією з причин побудови історично першим Х- променевого томографа, хоч дослідження проводилися спочатку над радіоактивними випромінюваннями.
, тобто, щоб виміряні значення p були рівними значенням інтеґралів від функції розподілу речовини всередині об’єкту дослідження по многовиду (прямих). Найближче від такої ідеальної моделі лежить Х-променева томоґрафія, бо Х- фотони (або, як їх ще називають, рентгенівські гама-кванти), якщо знехтувати їх розсіянням на ядрах молекул досліджуваної речовини, вторинними ефектами поширюються прямолінійно. Крім того, ступінь поглинання фотонів при проходження через речовину є інтеґральною характеристикою від лінійного коефіцієнта поглинання Х-променів. Побудувавши відповідну вимірювальну систему, можна добитись досить точної відповідності операторів T та R. Це стало однією з причин побудови історично першим Х- променевого томографа, хоч дослідження проводилися спочатку над радіоактивними випромінюваннями. , (5.6)
, (5.6) — векторний диференціальний оператор, r — просторові координати, W — кутові координати, Е — енергія частинок (фотонів);
— векторний диференціальний оператор, r — просторові координати, W — кутові координати, Е — енергія частинок (фотонів);  — функція розподілу фотонів по простору r, напрямах W та енергіях Е всередині об’єкту;
— функція розподілу фотонів по простору r, напрямах W та енергіях Е всередині об’єкту;  — функція розподілу фотонів від джерела X-випромінювання; f (r, E) — характеристика середовища;
— функція розподілу фотонів від джерела X-випромінювання; f (r, E) — характеристика середовища;  — макросічення релеївського та комптонівського розсіювання. Потік фотонів розкладається в ряд Наймана
— макросічення релеївського та комптонівського розсіювання. Потік фотонів розкладається в ряд Наймана , (5.7)
, (5.7) та функції
та функції 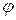 і
і  набирають вигляду:
набирають вигляду: ,
,  ,
,  .
. . (5.8)
. (5.8) , (5.9)
, (5.9) .
. і замінивши
і замінивши  , де
, де  — нормальні координати на площині, отримаємо:
— нормальні координати на площині, отримаємо: , (5.10)
, (5.10)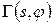 — лінії поширення випромінювання. Як видно з виразу (5.10), кількість зареєстрованих на виході з біооб’єкта фотонів експоненційно залежить від інтеґрального коефіцієнта ослаблення Х-випромінювання вздовж лінії проходження цього випромінювання через біооб’єкт.
— лінії поширення випромінювання. Як видно з виразу (5.10), кількість зареєстрованих на виході з біооб’єкта фотонів експоненційно залежить від інтеґрального коефіцієнта ослаблення Х-випромінювання вздовж лінії проходження цього випромінювання через біооб’єкт.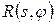 :
: , (5.11)
, (5.11) . (5.12)
. (5.12) , (5.13)
, (5.13)


