Поняття про зворотні задачі математичної фізики
Представимо біооб’єкт у фізичному полі схемою „вхід-вихід” (рис. 6.1), де f — фізичне поле до об’кту, „вхід” (його математична модель — функція, або вектор), p — поле після об’єкту, ”вихід” (математична модель — функція, або вектор), T — об’єкт (математична модель — оператор, матриця). Такій схемі адекватною є математична модель — операторне рівняння 1) відомі характеристика f поля на „вході” біооб’єкту та його функціональна характеристика T, потрібно знайти характеристику p поля на „виході” біооб’єкта; 2) ідентифікації, відомі „вхід” f, „вихід” p, потрібно знайти характеристику T; 3) відомо „вихід” p та характеристику T, потрібно знайти „вхід” f — обернена задача, її розв’язок знаходиться за формулою:
Основна задача томографії за схемою рис. 6.1 набирає вигляду
де Для розв’язування задач даного класу потрібно знайти обернений оператор
З математичної точки зору, основна задача комп'ютерної томографії — реконструкція деякої функції в тривимірному просторі Â 3 за відомими значеннями її інтеґралів вздовж певних прямих ліній або площин. В проблемі реконструкції функції виділяються три аспекти. По-перше, потрібно забезпечити достатню степінь представлення досліджуваного перерізу об'єкту отриманими проекційними даними. По-друге, бажано забезпечити малу чутливість процесу реконструкції до похибок проекційних даних. І, нарешті, необхідно побудувати метод реконструкції [17].
Основна задача томоґрафії, як і більшість обернених задач, належить до класу некоректних задач, тому при її розв’язанні існує ряд математичних проблем [11]. Розглянемо гільбертові простори F та P, і T — лінійний обмежений оператор, що діє з F в P (рис. 6.2). Задача полягає в тому, щоб, знаючи Для некоректно поставленої задачі обернений оператор
|

 Рис. 6.1 Схема впливу біооб’єкту на фізичне поле
Рис. 6.1 Схема впливу біооб’єкту на фізичне поле
 . Залежно від того, що у цьому виразі є невідомим, а що — відомим, виникають задачі:
. Залежно від того, що у цьому виразі є невідомим, а що — відомим, виникають задачі: . (6. 1)
. (6. 1) , (6. 2)
, (6. 2)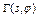 – границя перерізу,
– границя перерізу, 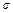 – елемент перерізу. Інтеґральний оператор T характеризує схему сканування, джерела випромінювання та взаємодію випромінювання з речовиною біооб’єкта:
– елемент перерізу. Інтеґральний оператор T характеризує схему сканування, джерела випромінювання та взаємодію випромінювання з речовиною біооб’єкта:  . Для конкретного томоґрафа він є відомим. Основна задача томоґрафії полягає в тому, щоб за відомим радонівським образом
. Для конкретного томоґрафа він є відомим. Основна задача томоґрафії полягає в тому, щоб за відомим радонівським образом 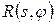 знайти характеристики біооб’єкта
знайти характеристики біооб’єкта  , тобто за поданою вище класифікацією, ця задача відноситься до класу обернених задач.
, тобто за поданою вище класифікацією, ця задача відноситься до класу обернених задач.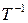 і тоді, за відомим радонівським образом
і тоді, за відомим радонівським образом  . (6. 3)
. (6. 3)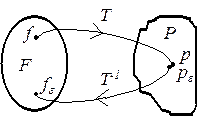 Рис. 6.2
Рис. 6.2
 , знайти
, знайти 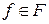 , для якого
, для якого  , де
, де  близьке до p. Рівняння, які описують некоректні задачі або взагалі не мають розв'язків, або мають неоднозначні чи нестійкі розв'язки. За умови наявності у проекційних даних похибок випадкового характеру, які можуть бути спричинені нестабільністю параметрів досліджуваного біооб’єкта, квантовою природою Х-випромiнювання, за допомогою якого формується зображення, похибками апаратури, розв'язок задачі реконструкції буде нестійким.
близьке до p. Рівняння, які описують некоректні задачі або взагалі не мають розв'язків, або мають неоднозначні чи нестійкі розв'язки. За умови наявності у проекційних даних похибок випадкового характеру, які можуть бути спричинені нестабільністю параметрів досліджуваного біооб’єкта, квантовою природою Х-випромiнювання, за допомогою якого формується зображення, похибками апаратури, розв'язок задачі реконструкції буде нестійким.


