Реґуляризаційні множники і фільтри
Наведемо приклади можливих реґуляризаційних множників, що використовуються при реконструкції томоґрафічних зображень:
де — параметр реґуляризації ( ³ 0), якщо = 0, тоді реґуляризація не проводиться, чим більше значення — тим " сильніша" реґуляризація. Вибір конкретного виду реґуляризацiйного множника залежить від характеристик зображення та шуму i потребує детального дослідження. Реґуляризацiйний множник є функцією просторової частоти та параметра реґуляризацiї . При =0 реґуляризацiя не проводиться, із збільшенням зменшується вплив шумів, але втрачається частина інформації. Вибір конкретного значення пов'язаний з очікуваною інтенсивністю спотворень зображення на основі апріорної інформації про досліджуваний біооб’єкт та характеристики похибок. Вибір оптимального значення параметра реґуляризацiї можна здійснювати принаймні трьома шляхами: — шляхом обчислення на основі апріорних відомостей про зображення, що реконструюється; — з допомогою ітераційної процедури оптимізації; — при допомозі ручного підбору параметра реґуляризацiї. Перший спосіб вибору параметра реґуляризацiї може розглядатись як оптимальна фільтрація згідно певного критерію: співвідношення сигнал / шум, мінімальної середньоквадратичної похибки тощо. Проте цей спосіб не має широкого практичного застосування, бо часто ми не маємо наперед відомих об'єктивних даних про характеристики зображення досліджуваного біооб’єкта та шумів, що накладаються на проекційні дані. У другому методі вибір оптимального значення параметра реґуляризацiї здійснюються виконанням ітераційної процедури. Розв'язує ться задача оптимізації, параметром оптимізації виступає . Питання вибору критерію оптимізації залишається відкритим. Традиційні критерії якості (відношення сигнал/ шум, середньоквадратичне відхилення) для томоґрафiчних зображень не завжди підходять. Для їх використання зображення повинно бути стаціонарним i мати закони розподілу імовірності значень випадкових величин близькі до нормального розподілу. Крім перерахованих вище недоліків, ітераційний метод потребує значних обчислювальних ресурсів та часових затрат. Можливий ще варіант ітераційної реґуляризації, що ґрунтується на використанні ітераційного методу розв’язування основного рівняння томоґрафії:
де Bi, Ci — неперервні лінійні оператори [15, стор. 102]. Третій спосіб дещо подібний до другого, проте оцінку якості зображення проводить інженер-оператор. " Оптимальне" зображення одержується після виконання кількох циклів реконструкції з різними значеннями параметра . Оператор, аналізуючи отримані зображення i підбираючи значення , може вибрати " найкраще" значення параметра реґуляризацiї. Проте, такий метод є ефективним на етапі експериментальних досліджень.
|

 , (6. 7)
, (6. 7) , (6. 8)
, (6. 8) (6. 9)
(6. 9) (6. 10)
(6. 10)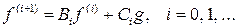 , (6. 11)
, (6. 11)


