Періодичні сигнали, або сигнали зі скінченним (фінітним) носієм, які можна періодично продовжити, можуть бути представлені за допомогою розкладу в ряд Фур’є [2, стор. 47]. Якщо сигнал 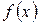 має фінітний спектр
має фінітний спектр 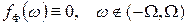 , властивість (е), то цей спектр можна розкласти в ряд Фур’є, коефіцієнти якого будуть з точністю до відповідних масштабних множників дискретними відліками сиґналу
, властивість (е), то цей спектр можна розкласти в ряд Фур’є, коефіцієнти якого будуть з точністю до відповідних масштабних множників дискретними відліками сиґналу 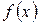 (рис. 7.2). Таким чином сиґнал з фінітним спектром можна представити з допомогою дискретних відліків, тобто дискретизувати. За теоремою Котельникова (в іноземній літературі — Уітекера-Найквіста-Шенона), сиґнал
(рис. 7.2). Таким чином сиґнал з фінітним спектром можна представити з допомогою дискретних відліків, тобто дискретизувати. За теоремою Котельникова (в іноземній літературі — Уітекера-Найквіста-Шенона), сиґнал 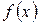 зі скінченною енерґією та фінітним спектром
зі скінченною енерґією та фінітним спектром  може бути представлений у вигляді ряду (ряду Котельникова) [2], стор. 58-63; [3], стор. 121-124:
може бути представлений у вигляді ряду (ряду Котельникова) [2], стор. 58-63; [3], стор. 121-124:
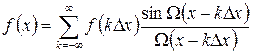 , (7. 3)
, (7. 3)
де інтервал дискретизації визначається із співвідношення: 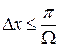 .
.
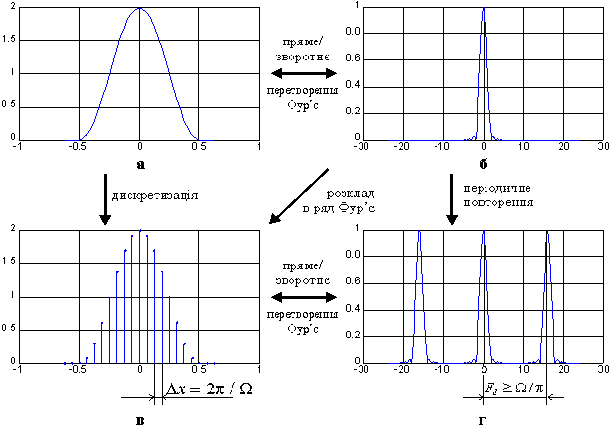 Рис. 7.2
Рис. 7.2
|
Для дискретизованих (дискретних) сигналів існує перетворення Фур’є, аналогічне перетворенню Фур’є неперервних сиґналів. Двовимірне пряме і обернене дискретне перетворення Фур’є (ДПФ) послідовності  записується такими виразами:
записується такими виразами:
 , (7. 4)
, (7. 4)
 , (7. 5)
, (7. 5)
де 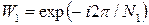 ,
, 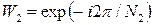 .
.
Воно зберігає всі властивості свого неперервного аналога і водночас має нові властивості, які дозволяють будувати ефективні алґоритми числення:
a) Дійсній послідовності  властиві співвідношення:
властиві співвідношення: 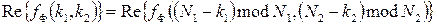 ,
, 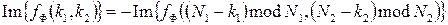 , тобто спектр дискретного сиґналу періодичний з періодом, рівним частоті дискретизації (послідовність
, тобто спектр дискретного сиґналу періодичний з періодом, рівним частоті дискретизації (послідовність 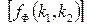 періодична з періодами N 1, N 2.)
періодична з періодами N 1, N 2.)
b) Двовимірне ДПФ матриці розмірністю N 1 на N 2 зводиться послідовного виконання N 1 одномірних ДПФ рядків матриці довжиною N 2 та виконання N 2 одномірних ДПФ стовпців матриці довжиною N 1:
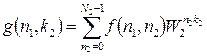 ,
,
 .
.
 Рис. 7.3
Рис. 7.3
|
Для обчислення двовимірного ДПФ матриці розміром N 1 на N 2 потрібно виконати (N 1* N 2)2 множень комплексних чисел. Врахування симетрій в обчисленнях для послідовностей розміром 2 m уможливлює побудову алґоритму ДПФ, у якому двовимірне дискретне перетворення Фур’є виконується лише 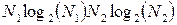 множеннями, що значно скорочує час обчислень, особливо при великих масивах даних. Такий алґоритм дістав назву алґоритм швидкого перетворення Фур’є (ШПФ, російською — БПФ, англійською — FFT). Для виконання одновимірного ШПФ потрібно
множеннями, що значно скорочує час обчислень, особливо при великих масивах даних. Такий алґоритм дістав назву алґоритм швидкого перетворення Фур’є (ШПФ, російською — БПФ, англійською — FFT). Для виконання одновимірного ШПФ потрібно 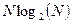 множень. Вигляд структури алґоритму ШПФ наведено на рис. 7.3 (
множень. Вигляд структури алґоритму ШПФ наведено на рис. 7.3 ( послідовних відліків сигналу, виконується
послідовних відліків сигналу, виконується  проходів (зліва-направо) елементарною ланкою обчислень, що носить назву „метелик” (butterfly), кроками знизу-вверх; останній прохід — сортування (перестановка) елементів відліків).
проходів (зліва-направо) елементарною ланкою обчислень, що носить назву „метелик” (butterfly), кроками знизу-вверх; останній прохід — сортування (перестановка) елементів відліків).

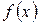 має фінітний спектр
має фінітний спектр 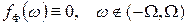 , властивість (е), то цей спектр можна розкласти в ряд Фур’є, коефіцієнти якого будуть з точністю до відповідних масштабних множників дискретними відліками сиґналу
, властивість (е), то цей спектр можна розкласти в ряд Фур’є, коефіцієнти якого будуть з точністю до відповідних масштабних множників дискретними відліками сиґналу  може бути представлений у вигляді ряду (ряду Котельникова) [2], стор. 58-63; [3], стор. 121-124:
може бути представлений у вигляді ряду (ряду Котельникова) [2], стор. 58-63; [3], стор. 121-124: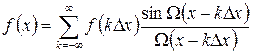 , (7. 3)
, (7. 3)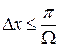 .
. Рис. 7.2
Рис. 7.2
 записується такими виразами:
записується такими виразами: , (7. 4)
, (7. 4) , (7. 5)
, (7. 5)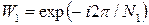 ,
, 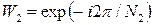 .
.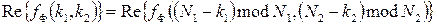 ,
, 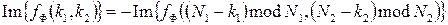 , тобто спектр дискретного сиґналу періодичний з періодом, рівним частоті дискретизації (послідовність
, тобто спектр дискретного сиґналу періодичний з періодом, рівним частоті дискретизації (послідовність 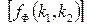 періодична з періодами N 1, N 2.)
періодична з періодами N 1, N 2.)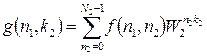 ,
, .
. Рис. 7.3
Рис. 7.3
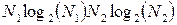 множеннями, що значно скорочує час обчислень, особливо при великих масивах даних. Такий алґоритм дістав назву алґоритм швидкого перетворення Фур’є (ШПФ, російською — БПФ, англійською — FFT). Для виконання одновимірного ШПФ потрібно
множеннями, що значно скорочує час обчислень, особливо при великих масивах даних. Такий алґоритм дістав назву алґоритм швидкого перетворення Фур’є (ШПФ, російською — БПФ, англійською — FFT). Для виконання одновимірного ШПФ потрібно 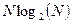 множень. Вигляд структури алґоритму ШПФ наведено на рис. 7.3 (
множень. Вигляд структури алґоритму ШПФ наведено на рис. 7.3 ( послідовних відліків сигналу, виконується
послідовних відліків сигналу, виконується  проходів (зліва-направо) елементарною ланкою обчислень, що носить назву „метелик” (butterfly), кроками знизу-вверх; останній прохід — сортування (перестановка) елементів відліків).
проходів (зліва-направо) елементарною ланкою обчислень, що носить назву „метелик” (butterfly), кроками знизу-вверх; останній прохід — сортування (перестановка) елементів відліків).


