В Х-променевому томоґрафі проекційні дані є дискретними відліками для фіксованого числа кутів p (типове значення p =512), тобто відбувається дискретизація радонівського образу за кутом. Крім того, значення інтенсивності Х-випромінювання записуються для фіксованго числа положень детектора q (у випадку одного детектора) або фіксованою кількістю детекторів q (у деяких томоґрафах). В будь-якому випадку ми маємо справу з матрицею дискретних даних, яка представляє радонівський образ зображення:  . В алгоритмі реконструкції на основі теореми про центральне січення для кожного значення кута знаходиться одновимірне ШПФ від послідовності
. В алгоритмі реконструкції на основі теореми про центральне січення для кожного значення кута знаходиться одновимірне ШПФ від послідовності 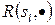 отриманої для даного кута. Після цього проводиться інтерполяція значень просторового спектру на прямокутній сітці з кроком
отриманої для даного кута. Після цього проводиться інтерполяція значень просторового спектру на прямокутній сітці з кроком  за отриманими одновимірними спектрами радонівського образу для всіх кутів
за отриманими одновимірними спектрами радонівського образу для всіх кутів  . І, нарешті, виконується двовимірне обернене ШПФ для отримання зображення. Використання алґоритму ШПФ приводить до того, що даний метод реконструкції є одним з найшвидших.
. І, нарешті, виконується двовимірне обернене ШПФ для отримання зображення. Використання алґоритму ШПФ приводить до того, що даний метод реконструкції є одним з найшвидших.
Точність реконструкції залежить як від методу інтерполяції з полярної сітки в прямокутну, так і від вибору параметрів дискретизації. Відомо, що чим вища частота дискретизації, тобто, чим менший інтервал дискретизації  , тим вища точність представлення неперервної функції її відліками. Проте, характеристики апаратури, які визначаються умовами її застосування, можуть не дозволити отримати проекційні дані та проводити реконструкцію для кількості точок, більшої, ніж, наприклад, 210. Якщо спектр функції відомий, то вибір інтервалу дискретизації можна вибрати за критерієм Найквіста-Котельникова-Шеннона:
, тим вища точність представлення неперервної функції її відліками. Проте, характеристики апаратури, які визначаються умовами її застосування, можуть не дозволити отримати проекційні дані та проводити реконструкцію для кількості точок, більшої, ніж, наприклад, 210. Якщо спектр функції відомий, то вибір інтервалу дискретизації можна вибрати за критерієм Найквіста-Котельникова-Шеннона:  , де
, де  — частота найвищої гармоніки. Тобто, інтервал дискретизації зображення вибирають таким, щоб він був в два рази меншим від розміру мінімального елемента зображення, який необхідно розрізняти будь-де по всьому зображенні.
— частота найвищої гармоніки. Тобто, інтервал дискретизації зображення вибирають таким, щоб він був в два рази меншим від розміру мінімального елемента зображення, який необхідно розрізняти будь-де по всьому зображенні.

 . В алгоритмі реконструкції на основі теореми про центральне січення для кожного значення кута знаходиться одновимірне ШПФ від послідовності
. В алгоритмі реконструкції на основі теореми про центральне січення для кожного значення кута знаходиться одновимірне ШПФ від послідовності 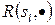 отриманої для даного кута. Після цього проводиться інтерполяція значень просторового спектру на прямокутній сітці з кроком
отриманої для даного кута. Після цього проводиться інтерполяція значень просторового спектру на прямокутній сітці з кроком  за отриманими одновимірними спектрами радонівського образу для всіх кутів
за отриманими одновимірними спектрами радонівського образу для всіх кутів  . І, нарешті, виконується двовимірне обернене ШПФ для отримання зображення. Використання алґоритму ШПФ приводить до того, що даний метод реконструкції є одним з найшвидших.
. І, нарешті, виконується двовимірне обернене ШПФ для отримання зображення. Використання алґоритму ШПФ приводить до того, що даний метод реконструкції є одним з найшвидших. , тим вища точність представлення неперервної функції її відліками. Проте, характеристики апаратури, які визначаються умовами її застосування, можуть не дозволити отримати проекційні дані та проводити реконструкцію для кількості точок, більшої, ніж, наприклад, 210. Якщо спектр функції відомий, то вибір інтервалу дискретизації можна вибрати за критерієм Найквіста-Котельникова-Шеннона:
, тим вища точність представлення неперервної функції її відліками. Проте, характеристики апаратури, які визначаються умовами її застосування, можуть не дозволити отримати проекційні дані та проводити реконструкцію для кількості точок, більшої, ніж, наприклад, 210. Якщо спектр функції відомий, то вибір інтервалу дискретизації можна вибрати за критерієм Найквіста-Котельникова-Шеннона:  , де
, де  — частота найвищої гармоніки. Тобто, інтервал дискретизації зображення вибирають таким, щоб він був в два рази меншим від розміру мінімального елемента зображення, який необхідно розрізняти будь-де по всьому зображенні.
— частота найвищої гармоніки. Тобто, інтервал дискретизації зображення вибирають таким, щоб він був в два рази меншим від розміру мінімального елемента зображення, який необхідно розрізняти будь-де по всьому зображенні.


