Методи цифрової фільтрації
На основі виразу згортки реалізуються цифрові фільтри зі скінченною імпульсною характеристикою (СІХ-фільтри, в англомовній літературі
Довжину імпульсної характеристики СІХ фільтрів можна зменшити у порівнянні з наведеною вже величиною М, вибираючи відповідне її значення таким, що забезпечується потрібна точність фільтрації. Інший метод цифрової фільтрації базується на використанні прямого і оберненого перетворення Фур’є. Оскільки в частотній області Ще один метод цифрової фільтрації — рекурсивний обчислювальний метод розв’язування диференційного (difference — різниця, англ.) рівняння. Такі цифрові фільтри мають нескінченну імпульсну характеристику (НІХ, IIR — infinite impulse response, БИХ — рос.):
Коли виконаємо z – перетворення від рівняння (8.2), то отримаємо вираз функції передачі фільтра:
Згортка отримується для представлення фільтру як системи типу вхід-вихід з міркувань, що система лінійна, отже має імпульсну характеристику і сума зсунутих відгуків на кожен вхідний відлік буде вихідним сиґналом. Тоді h — імпульсна характеристика системи, а обчислення згортки — метод побудови фільтра. У рекурсивному фільтрі застосовано метод розв’язування диференційного (різницевого) рівняння, дискретного варіанту неперервного, диференціального (differential) рівняння. Вираз нагадує дві згортки. Але Описані методи цифрової фільтрації та методи, побудовані на ще інших представленнях лінійних систем (вхід-вихід, у просторі змінних стану, диференціальними рівняннями, хвилевими рівняннями тощо) є еквівалентними математично. Проте їх застосування при побудові алґоритмів цифрової обробки сиґналів чи зображень з врахуванням можливостей представлення даних та виконання операцій у процесорі приводить до різних практичних результатів. Різні алґоритми забезпечують різну точність, різну кількість необхідних операцій (складність), і відповідно різну швидкодію, різну розрядність даних та кількість коефіцієнтів, що виливається в обсяг пам’яті. Зрештою, реалізація певних видів обробки деякими методами є просто неможливою (внаслідок фізичних, енерґетичних чи інших обмежень), тоді як іншими — здійснюється з мінімальними затратами. Особливий випадок є використання фільтрації при розв’язанні некоректних задач, де в залежності від варіанту реалізації та параметрів фільтра розв’язок може " збігатися" або бути " розбіжним", нестійким.
|

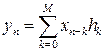 ,
,  . (8. 1)
. (8. 1) , то, маючи відліки сиґналу
, то, маючи відліки сиґналу  , беремо від нього дискретне перетворення Фур’є, множимо результат цього перетворення на функцію передачі фільтра H і отримуємо Y, від якого беремо обернене перетворення Фур’є й отримуємо
, беремо від нього дискретне перетворення Фур’є, множимо результат цього перетворення на функцію передачі фільтра H і отримуємо Y, від якого беремо обернене перетворення Фур’є й отримуємо  . На вхід цифрового фільтру подається і з виходу відбирається послідовності закодованих (двійковим кодом) значень відліків сигналу. Для того, щоб можна було використовувати такий алгоритм цифрової фільтрації, до сиґналів повинні ставитись певні вимоги. Наприклад, тривалість сиґналу має бути обмеженою, тоді легко виконувати перетворення Фур’є. Інакше потрібно використовувати вікна, для вирізання з " довгої" реалізації сиґналу окремих його вибірок. Це у свою чергу ставить вимогу до стаціонарності сигналу та його детермінованості.
. На вхід цифрового фільтру подається і з виходу відбирається послідовності закодованих (двійковим кодом) значень відліків сигналу. Для того, щоб можна було використовувати такий алгоритм цифрової фільтрації, до сиґналів повинні ставитись певні вимоги. Наприклад, тривалість сиґналу має бути обмеженою, тоді легко виконувати перетворення Фур’є. Інакше потрібно використовувати вікна, для вирізання з " довгої" реалізації сиґналу окремих його вибірок. Це у свою чергу ставить вимогу до стаціонарності сигналу та його детермінованості.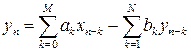 ;
; 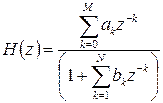 . (8. 3)
. (8. 3) ,
, 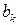 є параметри (коефіцієнти) різницевого рівняння, а не відліки імпульсної характеристики.
є параметри (коефіцієнти) різницевого рівняння, а не відліки імпульсної характеристики.


