Цифрова фільтрація в часовій та просторовій областях
Відомо, що для аналогового лінійного фільтру (рис. 9.1), за умови обмеженості енергій сигналу на його вході та його відгуку на дельта-сигнал (що в термінах математичних моделей їх означає інтегрованість з квадратом функцій, якими сигнал та відгук адекватно моделюються) існує таке співвідношення між лапласівськими образами вихідного і вхідного сиґналів:
де H (s), — функція передачі фільтру,
де У виразах (9.1, 9.2) величини Ω і t є дійсними числами. Їх назви, відповідно, частота і час (одиниці вимірювання — Гц та сек.). Проте, в томографії, вони можуть бути величинами просторовими — наприклад, просторовою частотою та віддаллю (одиниці вимірювання 1/м та м).
Одним з прикладів застосування згортки є математичне моделювання процесу обробки зображення деяким оптичним пристроєм, залежність чутливості якого від кута падіння променів має вигляд, зображений на рис. 9.3 (тоді відповідні одиниці вимірювання аргументів у виразах (9.1, 9.2) будуть, наприклад, 1/радіан та радіан). Якщо таким пристроєм сканувати зображення, то вихідне зображення буде результатом згортки вхідного зображення з функцією чутливості оптичного пристрою (тоді згортка є оптичною низькочастотною фільтрацією зображення, наприклад, перед його дискретизацією). В комп’ютерному томоґрафі також застосовується подібна обробка, наприклад, при „оцифровуванні” проекційних даних перед їх аналогово-цифровим перетворенням — АЦП, (analog-digital conversion — ADC, англ.). Для цифрової обробки значення дискретних сигналів кодують двійковим кодом, наприклад, з фіксованою точкою, типу знак-модуль або доповнюючим (комплементарним). Якщо сигнали цифрові, то вираз згортки аналоґічно до виразу (9.2) набуває вигляду:
де значком
де Аналогічно до виразу (9.2) одновимірної згортки можна записати формулу згортки і для двовимірних зображень:
та її цифровий варіант
де
|

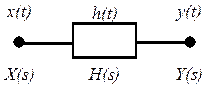 Рис. 9.1
Модель аналогового фільтру типу „вхід-вихід”
Рис. 9.1
Модель аналогового фільтру типу „вхід-вихід”
 , (9.1)
, (9.1) . З властивості добутку лапласівських образів [1, табл. 2.2] випливає, що
. З властивості добутку лапласівських образів [1, табл. 2.2] випливає, що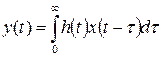 , (9.2)
, (9.2)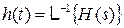 — обернене перетворення Лапласа від функції передачі фільтру, або (у фізичній інтерпретації) відгук фільтру на
— обернене перетворення Лапласа від функції передачі фільтру, або (у фізичній інтерпретації) відгук фільтру на 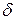 - подібний сигнал (рис. 9.2). У виразі (9.2) інтеграл
- подібний сигнал (рис. 9.2). У виразі (9.2) інтеграл 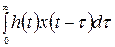
 за означенням є оператором згортки; інше його позначення — x (t)* h (t).
за означенням є оператором згортки; інше його позначення — x (t)* h (t). Рис. 9.2
Відгук фільтра на
Рис. 9.2
Відгук фільтра на  Рис. 9.3
Залежність чутливості h оптичного пристрою від кута падіння променів Θ
Рис. 9.3
Залежність чутливості h оптичного пристрою від кута падіння променів Θ
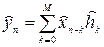 ,
,  , (9.3)
, (9.3)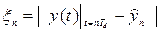 ,
,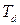 — період дискретизації. Імпульсна характеристика завжди скінченна, оскільки, починаючи з деякого n всі значення її представляються бітом молодшого розряду її двійкового коду. Крім того, обмежений об’єм пам’яті та потрібна швидкодія обчислень згортки також впливають на величину М.
— період дискретизації. Імпульсна характеристика завжди скінченна, оскільки, починаючи з деякого n всі значення її представляються бітом молодшого розряду її двійкового коду. Крім того, обмежений об’єм пам’яті та потрібна швидкодія обчислень згортки також впливають на величину М.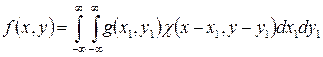 (9.4)
(9.4)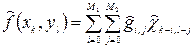 , (9.5)
, (9.5) .
.


