Метод зворотнього проектування на основі одновимірної згортки
Для реалізації реконструкції на основі зворотнього проектування попередньо профільтрованих за допомогою згортки одновимірних проекцій, потрібно знайти дискретні аналоги формул (4.19 - 4.21). Оскільки фізично неможливо реалізувати імпульсну характеристику (ядро) згортки нескінченної довжини (через кодування її значень двійковими кодами скінченної розрядності) і з врахуванням вимог до спектру імпульсної характеристики, які випливають з теореми Котельникова, будемо вважати, що спектральна енерґія будь-якої проекції близька до нуля при частотах, вищих деякої частоти
Якщо кожна проекція дискретизована з відстанню між сусідніми відліками t см, то щоби дискретизовані проекції не мали спотворень, пов’язаних з ефектом накладання просторових частот [5, 6], необхідно, щоб
Оскільки проекційні дані відбираються через інтервал дискретизації t і тому їх спектр перед цим відбором обмежується (антиалайзинговою фільтрацією), для цифрової обробки необхідно знати її імпульсну характеристику тільки в межах смуги частот. З (9.11) отримаємо
де n приймає цілі значення (додатні і від’ємні). В точках дискретизації
Для обмежених в смузі частот функцій, що задовольняють умову Дискретну згортку за формулою (9.13) можна реалізувати безпосередньо, однак вона буде обчислюватись значно довше, ніж при виконанні фільтрації в частотній області з використанням швидкого перетворення Фур’є (ШПФ). Проте, використовуючи спеціалізовані апаратні засоби (спецпроцесори), можна добитись того, що безпосереднє обчислення за формулою (9.13) буде здійснюватись швидше, ніж розрахунок в частотній області. При цьому якість реконструкції буде вищою, оскільки пряме-обернене перетворення Фур’є вносить додаткові похибки та артефакти. Крім того, для покращення якості реконструкції можна використати згладжування проекційних даних перед їх фільтруванням. Після фільтрування проекцій необхідно виконати другий крок алгоритму реконструкції — обчислити сумарну зворотню проекцію. Для цього потрібно знайти апроксимацію інтеґралу (4.21) числовими методами. Якщо число проекцій
Функція
Питання для самоперевірки
1. Які властивості повинна мати проекція Радона двовимірної функції для існування її лапласівського образу? 2. Чим відрізняються неперервна згортка від дискретної згортки? 3. Визначити імпульсну характеристику проективного перетворення. 4. Наведіть приклад обчислення згортки. 5. Які фільтри можна виконати за допомогою згортки? 6. Поясніть алґоритм 7. Назвіть переваги і недоліки алгоритму 8. У чому полягає метод зворотнього проектування згорткою? 9. Наведіть метод визначення дискретних значень ядра згортки. 10. Як перетворити у двійкові коди дискретні значення ядра згортки?
|

 . Тоді імпульсна характеристика фільтра — зворотне перетворення Фур’є від
. Тоді імпульсна характеристика фільтра — зворотне перетворення Фур’є від  в частотній області на смузі частот від -
в частотній області на смузі частот від -  . (9.10)
. (9.10) [7]. Підставляючи це значення
[7]. Підставляючи це значення  . (9.11)
. (9.11) (9.12)
(9.12)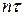 фільтровані проекції можуть бути отримані за допомогою дискретної згортки. Для дискретного випадку із співвідношення (4.20) випливає
фільтровані проекції можуть бути отримані за допомогою дискретної згортки. Для дискретного випадку із співвідношення (4.20) випливає . (9.13)
. (9.13) при
при  .
. досить велике і проекції рівномірно розподілені в секторі 180°, то рівняння (4.21) можна апроксимувати виразом
досить велике і проекції рівномірно розподілені в секторі 180°, то рівняння (4.21) можна апроксимувати виразом . (9.14)
. (9.14) являє собою відновлену апроксимацію функції
являє собою відновлену апроксимацію функції  . Зрозуміло, що внесок фільтрованої проекції з кутом
. Зрозуміло, що внесок фільтрованої проекції з кутом  в точку
в точку  відновлюваного зображення рівний
відновлюваного зображення рівний  . Як вже згадувалось в попередніх розділах, обчислення таких внесків одного
. Як вже згадувалось в попередніх розділах, обчислення таких внесків одного  у всі елементи зображення називається зворотнім проектуванням, а відповідні значення — зворотніми проекціями. Сума всіх зворотніх проекцій рівна
у всі елементи зображення називається зворотнім проектуванням, а відповідні значення — зворотніми проекціями. Сума всіх зворотніх проекцій рівна  в точку
в точку  . Значення s, однак, може не співпадати ні з одним із дискретних значень, для яких відомо
. Значення s, однак, може не співпадати ні з одним із дискретних значень, для яких відомо  достатньо взяти значення з найближчої сусідньої точки. При цьому, зворотнє проектування виконується з використанням малої кількості операцій множення.
достатньо взяти значення з найближчої сусідньої точки. При цьому, зворотнє проектування виконується з використанням малої кількості операцій множення. – фільтрації.
– фільтрації.


