Пряме та обернене перетворення Фур’є
При розв’язуванні задач обробки сиґналів використовуються їх ізоморфні (взаємнооднозначні) відображення. При цьому, зміни значень сигналу у часові, моделлю яких є функція дійсної змінної (або послідовність дійсних чисел), представляються за допомогою перетворення Фур’є функцією комплексної змінної (послідовністю комплексних чисел) [1]. Модуль такої функції є частотним спектром вихідної функції — амплітудами гармонічних функцій. Якщо вихідна функція періодична, то маємо ряд, членами якого є тригонометричні функції кратних частот („гармоніки”), — ряд Фур’є. Для розривних та неперіодичних функції розклад в ряд Фур’є розвинуто через інтегральні перетворення Фур’є, Лапласа та інші. В методах реконструкції на основі теореми про центральний переріз та на основі зворотнього проектування використовується пряме та обернене перетворення Фур’є (одно- або двовимірне). Перетворення Фур’є використовують також для побудови цифрових фільтрів в частотній області, оскільки тоді потрібна менша кількість операцій в порівнянні з фільтрами, побудованими в часовій області. Для функцій
Практично корисні та інтерпретовані є властивості перетворення Фур’є: a) Перетворення Фур’є дійсної функції
b) Результатом перетворення Фур’є парної функції є дійсна функція. c) Перетворення Фур’є дійсної парної функції дає дійсну парну функцію. d) Перетворення Фур’є дійсної непарної функції дає уявну непарну функцію. e) Перетворення Фур’є функції, яка на жодному інтервалі свого аргументу не нульова, є фінітною функцією (рис. 7.1, а) f) Перетворення Фур’є фінітної функції є функцією, яка на жодному інтервалі свого аргументу не нульова (рис. 7.1, б).
|

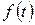 зі скінченною нормою
зі скінченною нормою  (або для сигналів зі скінченною енергією), заданих на осі
(або для сигналів зі скінченною енергією), заданих на осі  (або на нескінченному інтервалі часу)[14] існує пряме
(або на нескінченному інтервалі часу)[14] існує пряме  та обернене
та обернене  перетворення Фур’є. Аналогічно, для двовимірного випадку, означуються пряме та обернене перетворення Фур’є:
перетворення Фур’є. Аналогічно, для двовимірного випадку, означуються пряме та обернене перетворення Фур’є: , (7. 1)
, (7. 1) . (7. 2)
. (7. 2)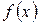 має властивість
має властивість  , тобто його дійсна частина — парна функція, а уявна — непарна.
, тобто його дійсна частина — парна функція, а уявна — непарна. Рис. 7.1
Рис. 7.1



