Застосування прямого і зворотнього перетворення Фур’є для розв’язання задачі томографії
З теореми про центральний переріз випливає ще один метод реконструкції, який, на відміну від попереднього, не потребує проведення двовимірного перетворення Фур’є, простіший в реалізації і для деяких томоґрафічних зображень дає кращу якість реконструкції [7]. Функцію
Інший варіант перетворення Фур’є можна отримати, перейшовши в частотній площині до полярної системи координат
отримаємо:
Підставивши
Введемо заміну
і позначимо внутрішній інтеґрал помножений на p через
тоді (3.11) набирає вигляду:
За формулами (3.12-3.14) можна записати такий метод відновлення зображення:
1) для радонівського образу 2) множимо 3) від результату знаходимо зворотнє перетворення Фур’є (3.13); 4) обчислюємо 5) інтеґруємо функцію I за кутом j (3.14); 6) міняємо кут j і повторюємо пп. (1-5).
За операціями пунктів (1-3) виконується фільтрація методом прямого-оберненого перетворення Фур’є. Даний метод реконструкції є варіантом реалізації методу зворотнього проектування. Якщо замінити фільтрацію в частотній області (див. пп. (1-3) на фільтрацію в просторовій області, то можна отримати ще один варіант реконструкції, що використовує операцію згортки функцій (аналог операції добутку функцій в ізоморфному просторі функцій-образів).
|

 можна виразити через її двовимірний спектр
можна виразити через її двовимірний спектр  за допомогою зворотнього двовимірного перетворення Фур’є:
за допомогою зворотнього двовимірного перетворення Фур’є: . (3. 8)
. (3. 8) . Зробивши заміну, виразивши просторові частоти через:
. Зробивши заміну, виразивши просторові частоти через: (3. 9)
(3. 9) . (3. 10)
. (3. 10) з формули (3.5) і врахувавши симетрію
з формули (3.5) і врахувавши симетрію  , отримаємо:
, отримаємо: . (3. 11)
. (3. 11) (3. 12)
(3. 12) , (3. 13)
, (3. 13) . (3. 14)
. (3. 14)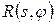 при фіксованому куті шукаємо спектр
при фіксованому куті шукаємо спектр  за допомогою одновимірного прямого Фур’є перетворення;
за допомогою одновимірного прямого Фур’є перетворення; ;
; (3.12);
(3.12);


