Ошибка! Ошибка связи
Рис. 2. 2. Схема ґеометричної інтерпретації визначення Радонівського образу двовимірної функції
Розв’язання задачі реконструкції функції за заданими її інтегралами уможливив стрімкий розвиток області комп'ютерної томографії, який розпочався наприкінці ХХ ст., що пов'язано з проґресом твердотільних мікроелектронних технологій та обчислювальної техніки. Нові технічні засоби забезпечували можливість реалізації алґоритмів реконструкції на основі зворотнього перетворення Радона. З цього часу активізується виробництво нових комп'ютерних томоґрафів, розширюється область їх застосувань, покращуються технічні параметри. Так, перший томоґраф мав такі технічні характеристики: число ракурсів сканувань — 180, число ліній проектування у ракурсі — 160, реконструювалось зображення 80 на 80 елементів, кожен розміром 3 мм; томоґраф, створений у 1975 р. Йорком та Маршалом забезпечував реконструкцію для матриці 160 на 160 елементів, а створений Евентом в 1976 р. — вже 256 на 256 (сучасні томоґрафи мають такі характеристики: розмірність зображення — 1024 на 1024 елементів, просторову роздільну здатність 15 ліній на см, роздільну здатність за густиною кращу 1%, час реконструкції близько 1 с. Залежно від конкретного виду томоґрафії (Х-променева, ЯМР тощо), значення функції розподілу густини мають різну фізичну природу (розмірність). Проте методи реконструкції зображень за проекційними даними мають багато спільного для різних видів томоґрафії. Алґоритми відновлення зображення плоского перерізу з експериментально отриманих його проекцій ґрунтуються на припущенні, що ці проекції є інтегралами по лініях від функції, що адекватно моделює розподіл речовини по площині перерізу. Степінь порушення цього припущення визначає інтенсивність артефактів, що проявляються на томоґрамі. Для Х-променевої комп’ютерної томоґрафії функція Пряма L, що задається параметрами s та
де Інтеграл від функції
де за допомогою дельта-функції В Х-променевій томоґрафії радонівський образ представляє всю сукупність проекцій досліджуваного об'єкта (функцій від s) під різними кутами Інший запис формули (2.2), що охоплює загальніший випадок інтеґрування по многовиду ліній (в тому числі й кривих), виглядає так
Повернемо систему координат на кут
то
Підставивши (2.5) в (2.2) та врахувавши, що
в якому інтеґрал одинарний, інтеґрування виконується по осі Основна задача томоґрафії полягає у реконструкції значень функції
|

 описує розподіл лінійного коефіцієнта ослаблення Х-випромінювання по площині. Значення цього коефіцієнта майже пропорційно залежать від густини речовини біооб’єкта, тому вважають, що Х-променеве томоґрафічне зображення відображає розподіл густини біооб’єкта в досліджуваній площині. При Х-променевій томоґрафії Х- промінь поширюється в основному прямолінійно, як зображено на рис. 2.2. Таким чином, цей рисунок відображає ґеометричну схему отримання проекційних даних, на якій ґрунтуються алґоритми реконструкції.
описує розподіл лінійного коефіцієнта ослаблення Х-випромінювання по площині. Значення цього коефіцієнта майже пропорційно залежать від густини речовини біооб’єкта, тому вважають, що Х-променеве томоґрафічне зображення відображає розподіл густини біооб’єкта в досліджуваній площині. При Х-променевій томоґрафії Х- промінь поширюється в основному прямолінійно, як зображено на рис. 2.2. Таким чином, цей рисунок відображає ґеометричну схему отримання проекційних даних, на якій ґрунтуються алґоритми реконструкції.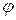 , визначає лінії інтеґрування (“проекціювання”, “сканування”). Її нормальне рівняння в координатах
, визначає лінії інтеґрування (“проекціювання”, “сканування”). Її нормальне рівняння в координатах  має вигляд
має вигляд , (2. 1)
, (2. 1) по множині прямимх L (по многовиду прямих
по множині прямимх L (по многовиду прямих  ), є її радонівським образом
), є її радонівським образом 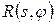 :
: , (2. 2)
, (2. 2) задано многовид прямих
задано многовид прямих  для фіксованого кута
для фіксованого кута  . (2. 3)
. (2. 3)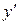 була паралельною до прямої L. Оскільки поворот системи координат у матричній формі має вигляд:
була паралельною до прямої L. Оскільки поворот системи координат у матричній формі має вигляд: , (2. 4)
, (2. 4)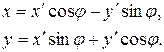 (2. 5)
(2. 5) , отримаємо основне рівняння томоґрафії
, отримаємо основне рівняння томоґрафії , (2. 6)
, (2. 6)


