На основі теореми про центральний переріз за формулами (3.2–3.5) можна побудувати метод відновлення зображення з проекцій використавши пряме і зворотнє перетворення Фур'є. Тобто, з радонівського образу отримати томоґрафічне зображення використавши ізоморфне перетворення в частотну область. Метод реконструкції складається з таких процедур:
1) N одновимірних перетворень проекцій при значеннях 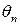 кута
кута  ,
, 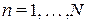 , за дискретним аналогом формули (3.2);
, за дискретним аналогом формули (3.2);
2) інтерполяції значень відліків на прямокутній сітці координат за значенням на полярній сітці в просторі частот (рис. 3.5), тобто перехід 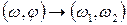 (дискретний варіант формули (3.5)). При інтерполяції враховується значення функції в одній або більшій кількості сусідніх точок, при цьому, чим більша кількість точок береться до уваги, тим складніший алґоритм обчислень. Так при врахуванні значень в чотирьох найближчих точках, інтерпольоване значення знаходиться за формулою:
(дискретний варіант формули (3.5)). При інтерполяції враховується значення функції в одній або більшій кількості сусідніх точок, при цьому, чим більша кількість точок береться до уваги, тим складніший алґоритм обчислень. Так при врахуванні значень в чотирьох найближчих точках, інтерпольоване значення знаходиться за формулою:
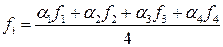 , (3. 7)
, (3. 7)
де 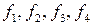 — значення функції у чотирьох найближчих точках, а коефіцієнти
— значення функції у чотирьох найближчих точках, а коефіцієнти 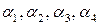 задаються відстанню до відповідної точки;
задаються відстанню до відповідної точки;
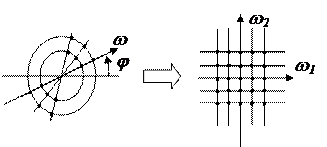 При інтерполяції точність знаходження значень в декартовій системі координат тим менша, чим далі ця точка знаходиться від початку координат.
При інтерполяції точність знаходження значень в декартовій системі координат тим менша, чим далі ця точка знаходиться від початку координат.
3) двовимірне обернене перетворення Фур'є функції 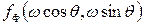 .
.
 До переваг цього алґоритму, в порівнянні з іншими алґоритмами реконструкції, відносяться використання стандартного математичного апарату прямого і оберненого перетворення Фур’є, простота для розуміння та висока швидкість обчислень при застосуванні алгоритму швидкого перетворення Фур’є (ШПФ)[12].
До переваг цього алґоритму, в порівнянні з іншими алґоритмами реконструкції, відносяться використання стандартного математичного апарату прямого і оберненого перетворення Фур’є, простота для розуміння та висока швидкість обчислень при застосуванні алгоритму швидкого перетворення Фур’є (ШПФ)[12].
Основний недолік методу — складність переходу від полярної системи координат до декартової, тому в реальних томоґрафах цей алґоритм мало застосовується.

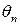 кута
кута  ,
, 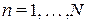 , за дискретним аналогом формули (3.2);
, за дискретним аналогом формули (3.2);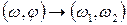 (дискретний варіант формули (3.5)). При інтерполяції враховується значення функції в одній або більшій кількості сусідніх точок, при цьому, чим більша кількість точок береться до уваги, тим складніший алґоритм обчислень. Так при врахуванні значень в чотирьох найближчих точках, інтерпольоване значення знаходиться за формулою:
(дискретний варіант формули (3.5)). При інтерполяції враховується значення функції в одній або більшій кількості сусідніх точок, при цьому, чим більша кількість точок береться до уваги, тим складніший алґоритм обчислень. Так при врахуванні значень в чотирьох найближчих точках, інтерпольоване значення знаходиться за формулою: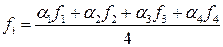 , (3. 7)
, (3. 7)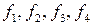 — значення функції у чотирьох найближчих точках, а коефіцієнти
— значення функції у чотирьох найближчих точках, а коефіцієнти 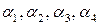 задаються відстанню до відповідної точки;
задаються відстанню до відповідної точки; При інтерполяції точність знаходження значень в декартовій системі координат тим менша, чим далі ця точка знаходиться від початку координат.
При інтерполяції точність знаходження значень в декартовій системі координат тим менша, чим далі ця точка знаходиться від початку координат.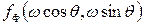 .
. До переваг цього алґоритму, в порівнянні з іншими алґоритмами реконструкції, відносяться використання стандартного математичного апарату прямого і оберненого перетворення Фур’є, простота для розуміння та висока швидкість обчислень при застосуванні алгоритму швидкого перетворення Фур’є (ШПФ)[12].
До переваг цього алґоритму, в порівнянні з іншими алґоритмами реконструкції, відносяться використання стандартного математичного апарату прямого і оберненого перетворення Фур’є, простота для розуміння та висока швидкість обчислень при застосуванні алгоритму швидкого перетворення Фур’є (ШПФ)[12].


