ЛОГИКА ОТНОШЕНИЙ

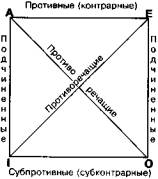
- раздел логики, изучающий свойства высказываний об отношениях между объектами различной природы. Элементарными высказываниями об отношениях являются высказывания вида akb, т. е. объект а находится в отношении k к объекту b, напр.: «а брат b», «а тяжелее b» и т. п. В зависимости от числа объектов, связанных тем или иным отношением, различают

двухместные, или бинарные, отношения, трехместные, или тернарные, отношения, напр.: «a находится между b и с»; и вообще n -местные, или n -арные, отношения. Особое значение имеют бинарные отношения, посредством которых определяют такие важнейшие понятия логики и математики, как «функция» и «операция». Вводя для бинарных отношений теоретико-множественные операции объединения (суммы), пересечения (произведения) и дополнения, получают «алгебру отношений», роль единицы в которой играют отношения эквивалентности (равенства, тождества). Отношения эквивалентности обладают следующими свойствами: а) рефлексивностью: для всякого х верно, что xkx, т. е. каждый объект находится в данном отношении к самому себе;

б) симметричностью: из xky следует ykx;

в) транзитивностью: из xky и ykz следует xkz.

Опираясь на различные свойства отношений, можно из одних высказываний об отношениях выводить другие высказывания. Напр., отношение «быть братом» симметрично, поэтому из высказывания «а брат b» можно сделать вывод о том, что «b брат а». В естественном языке трудность подобных выводов состоит в том, чтобы установить, обладает ли рассматриваемое отношение необходимым для вывода свойством. Напр., можно ли из высказывания «а теплее b» сделать вывод о том, что «b теплее а»? Нет, нельзя, т. к. отношение «быть теплее» не является симметричным. Но оно является транзитивным, потому из высказываний «а теплее b» и «b теплее с» можно вывести высказывание «а теплее с».

Значительный вклад в разработку Л.о. внес рус. логик С. И. Поварнин (1870—1952). В современной математической логике отношения выражаются посредством многоместных предикатов, напр.: «Брат (а, b)», «Больше (а, b)» и т. п. Поэтому Л. о. в настоящее время разрабатывается как часть логики предикатов.

ЛОГИКА ПРЕДИКАТОВ, или: Функциональная логика, теория квантификации, кванторная логика,

- основной раздел современной (математической, символической) логики, в котором описываются выводы, учитывающие внутреннюю (субъектно-предикатную) структуру высказываний. Л. п. является расширенным вариантом логики высказываний.

В Л. п. — в дополнение к средствам логики высказываний -вводятся логические операторы " («для всех») и $ («для некоторых» или «существует»), называемые кванторами общности и существования соответственно. Для выявления субъектно-предикатной структуры высказываний вводится бесконечный перечень индивидных переменных: х, у, z,..., х ¹, у ¹, z ^l,..., представляющих различные объекты, и бесконечный перечень предикатных переменных: Р, Q, R,..., Р ¹, Q ¹, Л¹,..., представляющих свойства и отношения объектов. Индивидные переменные принимают значения в произвольной (непустой) области; наряду с этими переменными могут вводиться индивидныеконстанты, или имена собственные.

Запись (" х) Р (х) означает «Всякий х обладает свойством Р»; ($ х) Р (х) - «Некоторые х обладают свойством Р»; ($ x) Q (xy) - «Существует х, находящийся в отношении Q с у» и т. п. Индивидная переменная, входящая в область действия квантора по этой переменной, называется связанной; переменная, не являющаяся связанной, называется свободной. Так, во всех трех приведенных формулах переменная х связана, в последней формуле переменная у свободна. Подлинной переменной является только свободная переменная: вместо нее можно подставить одно из ее значений и получить осмысленное выражение. Связанные переменные называются фиктивными.

Формула Л. п. называется общезначимой, если она истинна в каждой интерпретации. Тавтология логики высказываний является частным случаем общезначимой формулы. В Л. п., в отличие от логики высказываний, нет эффективного процесса, позволяющего для произвольно взятой формулы решить, является она общезначимой или нет.

Для Л. п. доказан ряд важных теорем, характеризующих ее основные свойства (см.: Непротиворечивость, Полнота, Разрешимость теории).

ЛОГИКА ЭПИСТЕМИЧЕСКАЯ (от греч. episteme - знание)

- раздел модальной логики, исследующий логические связи высказываний, включающих такие понятия, как «полагает» («убежден»), «сомневается», «отвергает», «знает», «доказуемо», «неразрешимо», «опровержимо» т. п.

Знание отличается от убеждения, или веры: знание всегда истинно, убеждение же может быть как истинным, так и ложным. Этому различию соответствует различие между двумя вариантами Л. э.: логикой знания и логикой убеждений. Каждая из этих «логик» слагается из логических систем, различающихся не только законами, но и исходными понятиями. Иногда к Л. э. относят лишь логику убеждений.

Одна из первых логик знания была сформулирована австрийским математиком и логиком К. Гёделем (1906-1978). Исходным термином ее является «доказуемо»; в числе ее законов положения:

· > > если высказывание доказуемо, оно истинно (доказать можно только истину, доказательств лжи не существует);

· > > логические следствия доказуемого также являются доказуемыми;

· > > если нечто доказуемо, то доказуемо, что оно доказуемо;

· > > логическое противоречие недоказуемо и т. п.

Другим примером логики знания может служить логика истины, устанавливающая такие законы, как:

· > > если высказывание истинно, то неверно, что его отрицание также истинно («Если истинно, что Земля вращается, то неверно, что истинно, будто она не вращается»);

· > > конъюнкция истинна, если и только если оба входящих в нее высказывания истинны («Истинно, что холодно и идет снег, только если истинно, что холодно, и истинно, что идет снег»), и т. п.

В логике убеждений в качестве исходного обычно принимается понятие «полагает» («убежден», «верит»), через него определяются понятия «сомневается» и «отвергает»:

· > > субъект сомневается в чем-то, если только он не убежден ни в этом, ни в противоположном;

· > > субъект отвергает нечто, если только он убежден в противоположном.

Среди законов логики убеждений положения:

· > > субъект полагает, что первое и второе, если и только если он полагает, что первое, и полагает, что второе («Субъект верит, что Марс - планета и что Луна - планета, только если он верит, что Марс — планета, и верит, что Луна — планета»);

· > > нельзя одновременно верить и сомневаться, быть убежденным и отвергать, сомневаться и отвергать;

· > > субъект или убежден, что дело обстоит так-то, или сомневается в этом, или отвергает это («Субъект или убежден, что Венера — звезда, или сомневается в этом, или отвергает это»);

· > > невозможно быть убежденным одновременно в ч.-л. и в противоположном («Нельзя верить как в то, что астрология наука, так и в то, что она не является наукой») и т. п.

Для понятий «знает», «истинно», «доказуемо» верно, что логические следствия известного также известны, истинного — истинны, доказуемого — доказуемы. Аналогичный принцип для понятия «убежден», кажущийся противоинтуитивным, получил название парадокса логическоговсеведения. Он утверждает, что человек убежден во всех логических следствиях, вытекающих из принимаемых им положений. Напр., если человек уверен в пяти постулатах геометрии Евклида, то, значит, принимает и всю эту геометрию, поскольку она вытекает из них. Но это не так. Соглашаясь с постулатами, человек может не знать доказательства теоремы Пифагора и потому сомневаться в том, что она верна.

Л.э. находит интересные приложения в теории познания и в методологии науки, в лингвистике, психологии и др.

ЛОГИСТИКА — в начале XX в. название формальной логики, изучаемой математическими методами, в частности с использованием аксиоматизации и формализации. Слово первоначально означало искусство вычисления или обычную арифметику. Г. Лейбниц употреблял его для обозначения «исчисления умозаключений», которое он пытался развить.

Термин вышел из употребления, уступив место терминам математическая логика, символическая логика или логика современная.

ЛОГИЦИЗМ — концепция, сводящая математику к логике. Согласно Л., логика и математика соотносятся между собой как части одной и той же науки: математика может быть получена из чистой логики без введения дополнительных основных понятий или дополнительных допущений. Под логикой при этом понимается теория дедуктивного рассуждения (см.: Дедукция).

Л. восходит к идее Г. Лейбница (1646—1716) о «сводимости математики к логике». Во второй половине прошлого века немецкий логик Г. Фреге (1848-1925) сформулировал арифметику чисто логически, но, столкнувшись с парадоксами, признал свою попытку безнадежной. В дальнейшем тезис Л. развивали англ. философы и логики Б. Рассел (1872-1970) и А. Уайтхед (1861-1947).

Против идеи, что математические понятия можно свести к логическим понятиям с помощью явных определений и затем вывести математические теоремы из логических аксиом, обычно выдвигаются следующие возражения. Прежде всего, для сведения математики к логике приходится принимать аксиомубесконечности, предполагающую существование бесконечных множеств. Сам Б. Рассел вынужден был признать, что она не является собственно логической. Далее, вывод математики из логики в какой-то степени содержит круг. Всегда имеются необоснованные предпосылки, которые должны быть приняты на веру или интуитивно. Можно попытаться уменьшить их число, но нельзя избавиться от них совсем. Различение, что из этих предпосылок относится к математике, а что - к логике, лежащей в ее основе, носит субъективный и по существу произвольный характер. И наконец, в 1931 г. К. Гёдель показал, что все системы аксиоматически построенной арифметики существенно неполны: их средствами невозможно доказать некоторые содержательные истинные арифметические утверждения. Основной тезис Л. следует, таким образом, признать опровергнутым.

Это не означает, что Л. был совершенно бесплодным. Его сторонники добились определенных успехов в прояснении основ математики. В частности, было показано, что математический словарь сводится к неожиданно краткому перечню основных понятий, которые принадлежат, как принято считать, словарю чистой логики. Вся существующая математика была сведена к сравнительно простой и унифицированной системе исходных, принимаемых без доказательства положений, или аксиом, и правил вывода из них следствий, или теорем.

Однако в целом Л. оказался утопической концепцией.

ЛОГИЧЕСКАЯ МАШИНА — механическое, электромеханическое или электронно-вычислительное устройство, предназначенное для полуавтоматического или автоматического решения широкого круга математических и логических задач, для управления технологическими и производственными процессами, для оптимальных экономических расчетов, для обработки массивов информации, которые мозг человека не в состоянии охватить, для моделирования форм человеческого мышления.

Попытки создать механические устройства для осуществления арифметических операций уходят в далекую древность. Первую логическую машину построил Раймунд Луллий (1235—1315). Его машина состояла из семи вращающихся вокруг одного центра кругов. На каждом из них были написаны слова, выражающие различные понятия, напр. «человек», «знание», «количество» и т. п., и логические операции, напр. «равенство», «противоречие» и т. п. Вращая круги, можно было получать разнообразные сочетания понятий. С помощью своей машины Луллий получал из заданных посылок силлогистические выводы. В первой половине XVII в. французский математик Б. Паскаль (1623-1662) сконструировал машину для выполнения арифметических операций. Идея машинизации процессов умозаключения была теоретически развита немецким философом и ученым Г. Лейбницем (1646-1716) в работе «Об искусстве комбинаторики». Первой подлинно Л. м. считается «демонстратор» Ч. Стенхопа (1753-1816), с помощью которого проверялись не только традиционные, но и т. наз. «числовые» силлогизмы. «Демонстратор» решал элементарные задачи традиционной логики.

Научные основы для создания современных Л. м. были заложены благодаря развитию математической логики и кибернетики, а техническая возможность их создания была обеспечена прогрессом в области электроники и автоматики. В 1944 г. в США была построена автоматическая вычислительная машина «Марк-1», имевшая электромагнитное реле и перфоленту, на которой записывались числа и указывались операции с ними. В 1945 г. Дж. фон Нейман предложил помещать закодированную программу вычислений в запоминающее устройство машины, что значительно расширило диапазон ее возможностей. С середины 50-х годов начали создаваться информационно-логические машины, способные хранить значительные записи информации, выбирать из них необходимые данные и производить не только математическую обработку информации, но и логические операции. Л. м. последующих поколений способны осуществлять миллиарды операций в секунду, различать простые рисунки, самообучаться, понимать простые фразы на естественном языке и решать самые разнообразные задачи во многих областях науки, техники, управления и т. д.

Принципиальная схема Л. м. включает следующие основные компоненты: 1. Входное устройство, преобразующее внешнюю информацию в последовательность электрических импульсов. 2. Выходное устройство, преобразующее электрические сигналы в последовательность воспринимаемых человеком знаков. 3. Запоминающее устройство, хранящее информацию и часто называемое просто «памятью» машины. Различают оперативную память, емкость которой сравнительно невелика, но отличается быстродействием, и долговременную, внешнюю память, с большим объемом, но меньшим быстродействием. 4. Арифметическое устройство, осуществляющее математические и логические действия. 5. Блок управления, обеспечивающий автоматическое выполнение программы, введенной в машину.

Все более широкое использование Л. м. позволяет человеку решать все более сложные задачи, освобождает его от рутинных мыслительных операций и делает человеческий труд все более творческим.

ЛОГИЧЕСКАЯ ПРАВИЛЬНОСТЬ — соответствие законам и правилам формальной логики. Обычно проводят различие между истинностью и правильностью человеческого мышления. Понятие истины характеризует мышление в его отношении к действительности: мысль, предложение истинны, если они соответствуют действительности. Понятие правильности характеризует мышление в его отношении к законам и правилам логики: рассуждение правильно, если в нем соблюдены все необходимые правила логики.

Различие между истинностью и правильностью отчетливо проявляется в тех случаях, когда формально правильное рассуждение приводит к ложному выводу. Напр., рассмотрим умозаключение:

Все металлы — твердые тела. Ртуть не является твердым телом.

Ртуть не является металлом.

Это умозаключение построено в форме простого категорического силлогизма, причем оно отвечает соответствующим правилам, т. е. правильно. Однако вывод является ложным. Это обусловлено ложностью первой посылки. Если рассуждение построено неправильно, то даже из истинных посылок мы можем получить как истину, так и ложь. Напр.:

Все тигры — полосаты.

Это животное - полосато.

Это животное — тигр.

Выводное суждение может быть как истинным, так и ложным, в зависимости от того, кто перед нами — полосатый тигр или полосатая зебра. Для того чтобы выводное знание было безусловно истинным, требуется, чтобы наше рассуждение опиралось на истинные посылки и было правильным. Правильность рассуждений можно контролировать, гораздо сложнее устанавливается истинность знания. Ученые прошлого часто приходили к ложным выводам не потому, что рассуждали неправильно, а потому, что посылки их были ложными.

ЛОГИЧЕСКАЯ ФОРМА — способ связи содержательных частей рассуждения (доказательства, вывода и т. п.). В соответствии с основным принципом логики, правильность рассуждения зависит только от его формы и не зависит от его конкретного содержания. Само название «формальная логика» подчеркивает, что эта логика интересуется только формой рассуждения. Л. ф. представляется посредством логических констант и переменных. Логические константы, подобные «и», «или», «если, то» и т. д., не имеют самостоятельного содержания, но с их помощью из одних содержательных выражений могут быть получены новые содержательные выражения. Переменные, входящие в Л. ф., представляют выражения, обладающие самостоятельным содержанием: высказывания, имена (см.: Символы собственные и несобственные).

Напр., высказывания «Все лошади едят овес» и «Все реки впадают в море» различны по своему содержанию, причем первое истинно, а второе ложно. Отвлекаясь от содержания высказываний, можно заменить их части переменными S и Р. Получим, что данные высказывания имеют одну и ту же логическую форму: «Все S есть Р». Содержательно разные высказывания «Если есть огонь, то есть дым» и «Если математика - наука, то она устанавливает законы» также имеют одинаковую логическую форму: «Если А, то В».

Следующие два вывода, различающиеся своим содержанием, совпадают по своей логической форме: «Если сейчас день, то светло. Сейчас день. Следовательно, светло» и «Если 13 - простое число, оно делится только на себя и на единицу. 13 - простое число. Следовательно, 13 делится только на себя на и на единицу». Заменив высказывания, входящие в данные выводы, переменными, получаем, что в обоих случаях рассуждение идет по одной и той же схеме: «Если А, то В. А. Следовательно, В». Это — схема правильного рассуждения: какие бы конкретные высказывания ни подставлялись вместо A и В, если посылки истинны, заключение также будет истинным (см.: Логическая правильность).

Различие между Л. ф. и содержанием не является абсолютным. То, что в одном случае считается относящимся к форме, в другом может оказаться содержательным компонентом рассуждения, и наоборот.

Интерес логики к Л. ф. не означает отвлечение ее от всякого содержания. Сама Л. ф. обладает определенным абстрактным содержанием, его иногда называют «формальным», чтобы отличить от «конкретного содержания». Скажем, форма «Все S есть Р» указывает, что у всякого предмета, обозначаемого буквой S, есть признак, обозначаемый буквой Р.

Понятие Л. ф. является центральным в логике. С ним связаны понятия логического закона, правила вывода, логического следования и др.

ЛОГИЧЕСКИЕ КОНСТАНТЫ, или: Логическиепостоянные, — термины, относящиеся к логической форме рассуждения (доказательства, вывода) и являющиеся средством передачи человеческих мыслей и выводов, заключений в любой области. К Л. к. относятся такие слова, как «не», «и», «или», «есть», «каждый», «некоторый» и т. п. Л. к. не имеют самостоятельного содержания. Сами по себе они ничего не описывают и ничего не обозначают. Вместе с тем они позволяют из одних содержательных выражений получать другие. Установление точного смысла Л. к. и выяснение самых общих законов, относящихся к ним, — одна из основных задач логики (см.: Логическая форма, Символы собственные и несобственные, Символика логическая).

ЛОГИЧЕСКИЕ ОПЕРАЦИИ - операции, посредством которых из простых высказываний образуются сложные, из простых терминов — сложные, из высказываний — термины, из терминов — высказывания и т. д.

К Л. о., позволяющим из одних высказываний получать другие высказывания, относятся конъюнкция («и», символически &), дизъюнкция («или», v), импликация («если, то», ->), эквивалентность («если и только если», =), отрицание («неверно, что», ~) и др. Так, если даны два произвольных высказывания A и В, из них с помощью конъюнкции получается сложное высказывание A & В, которое истинно, только когда A и B истинны; с помощью дизъюнкции получается сложное высказывание A v В, истинное, когда хотя бы одно из входящих в него высказываний истинно, и т. п. (см.: Логика высказываний).

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ АВТОМАТИКИ - устройства, реализующие некоторые простые логические функции и функциональные преобразования в машинах, самостоятельно работающих по заданной программе. Наиболее распространенным логическим элементом, применяемым в схемах управления автоматических устройств, является электромеханическое реле, реагирующее на определенные значения и изменения величин к.-л. параметра. Напряжение на его катушке является входным сигналом, состояние контактов реле (замкнутость или разомкнутость) — выходным сигналом.

Логические элементы являются одной из важнейших частей электронно-вычислительных машин. Они подразделяются на элементы, реализующие логическое отрицание, — схема «НЕ»; элементы, реализующие логическую конъюнкцию, — схема «И»; элементы, реализующие логическую дизъюнкцию, — схема «ИЛИ», и элементы, реализующие комбинированные логические операции. В сущности смысл работы логических элементов заключается в том, чтобы пропускать или не пропускать сигнал по той или иной цели, усиливать поступивший сигнал или не усиливать и т. п. Набор логических элементов позволяет электронно-вычислительной машине осуществлять преобразования информации в соответствии с преобразованиями формул в алгебре логики.

ЛОГИЧЕСКИЙ АНАЛИЗ - применение средств математической логики для обсуждения и решения философских и методологических проблем. Выражение проблемы в формальном языке придает ей точность и определенную ясность, что иногда способно облегчить поиск ее решения. При этом часто оказывается, что формальное выражение проблемы не вполне адекватно ее содержательному пониманию. Тогда мы пытаемся улучшить это выражение и сделать его более адекватным. Одновременно происходит и более глубокое содержательное уяснение анализируемой проблемы. Напр., когда А. Тарский строит точное формальное определение понятия истины, он применяет понятие истины к предложениям. Это дает повод поставить вопрос о том, чему мы приписываем понятие истины — предложениям или суждениям. Обсуждение этого вопроса позволяет более глубоко понять природу суждения и предложения.

Основы метода Л. а. были заложены в трудах немецкого математика и логика Г. Фреге и англ. логика и философа Б. Рассела. Однако широкое распространение он получил в трудах представителей логического позитивизма, которые провозгласили, что основной задачей философии является Л. а. языка науки. Несмотря на значительные успехи в решении отдельных проблем, достигнутые Р. Карнапом, К. Гемпелем, К. Рейхенбахом и др., представители логического позитивизма в общем не смогли использовать все эвристические возможности метода Л. а., т. к. в силу своих гносеологических установок ограничивали базис этого метода средствами экстенсиональной логики. В настоящее время метод Л. а. часто используется на различных этапах философско-методологического исследования: для более четкой постановки проблем, для выявления скрытых допущений той или иной точки зрения, для уточнения и сопоставления конкурирующих концепций, для их более строгого и систематического изложения и т. п. Следует лишь помнить об ограниченности этого метода и опасностях, связанных с его применением. Точность выражений, к которым приводит метод Л. а., часто сопровождается обеднением содержания. Простота и ясность формального выражения некоторой проблемы иногда может порождать иллюзию решения там, где еще требуются дальнейшие исследования и дискуссии. Трудности формального представления и заботы о его адекватности могут увести нас от обсуждений собственно философской или методологической проблемы и заставить заниматься техническими вопросами, лишенными философского смысла. Между прочим, так и случилось со многими методологическими проблемами логического позитивизма. Если же помнить об этом и рассматривать формальное выражение философско-методологической проблемы не как конечный результат, а как вспомогательное средство более глубокого философского анализа, как некоторый промежуточный этап в ходе философского исследования, то такие формальные выражения иногда могут оказаться полезными (см.: Логика научного познания). ЛОГИЧЕСКИЙ ЗАКОН, или: Закон л о г и к и, - выражение, содержащее только логические константы и переменные и являющееся истинным в любой (непустой) предметной области. Примером Л. з. может служить любой закон логики высказываний (скажем, непротиворечия закон, закон исключенного третьего, закон де Моргана, закон косвенного доказательства и т. п.) или логики предикатов.

Л. з. принято называть также (логической) тавтологией. В общем случае логическая тавтология — выражение, остающееся истинным, независимо от того, о каких объектах идет речь, или «всегда» истинное выражение. Напр., в выражение «Неверно, что р и не - р», представляющее непротиворечия закон, вместо переменной р должны подставляться высказывания. Все результаты таких подстановок («Неверно, что 11 - простое число и вместе с тем не является простым» и т. п.) являются истинными высказываниями. В выражение «Если для всех х верно, что х есть Р, то не существует х, не являющийся Р», представляющее закон логики предикатов, вместо переменной х должно подставляться имя объекта из любой (непустой) предметной области, а вместо переменной Р — некоторое свойство.

Все результаты таких подстановок представляют собой истинные высказывания («Если для всех людей верно, что они смертны, то не существует бессмертного человека», «Если каждый металл пластичен, то нет непластичных металлов» и т. п.).

Понятие Л. з. непосредственно связано с понятием логического следования: заключение логически следует из принятых посылок, если оно связано с ними логическим законом. Напр., из посылок «Если р, то q» и «Если q, то r» логически следует заключение «Если р, то r», поскольку выражение «Если (если р, то q, и если q, то r), то (если р, то r)» представляет собой транзитивности закон (скажем, из посылок «Если человек отец, то он родитель» и «Если человек родитель, то он отец или мать» по этому закону логически вытекает следствие «Если человек отец, то он отец или мать»).

Современная логика исследует логические законы только как элементы систем таких законов. Каждая из логических систем содержит бесконечное множество Л. з. и представляет собой абстрактную знаковую модель, дающую описание какого-то определенного фрагмента, или типа, рассуждений. Напр., бесконечное множество систем, обладающих существенной общностью и объединяемых в рамках модальной логики, распадается на эпистемическую логику, деонтическую логику, оценок логику, логику времени и др.

В современной логике построены логические системы, не содержащие закона непротиворечия (паранепротиворечивая логика), закона исключенного третьего, закона косвенного доказательства (интуиционистская логика) и т. д.

ЛОГИЧЕСКИЙ КВАДРАТ (квадрат противоположностей) - диаграмма, служащая для мнемонического запоминания некоторых логических соотношений между общеутвердительными (A), общеотрицательными (Е), частноутвердительными (I) и частноотрицательными суждениями (О). Логический квадрат показан на рисунке. Противоречащие, контрадикторные суждения (А и О; Е и I) не могут быть одновременно истинными и ложными: если одно из них истинно, то другое ложно. Так, если суждение «Все металлы являются электропроводными» (A) истинно, то суждение «Некоторые металлы не являются электропроводными» ложно. Если суждение «Некоторые металлы не являются твердыми» (О) истинно, то суждение «Все металлы являются твердыми» (А) ложно.

Противные суждения (A и Е), в отличие от противоречащих, могут оба оказаться ложными, но не могут быть оба истинными. Так, суждения «Все студенты являются шахматистами» (A) и «Ни один студент не является шахматистом» (Е) оба ложны. При истинности же одного из них второе является ложным. Так, если суждение «Все кенгуру являются млекопитающими» (A) истинно, то суждение «Ни один кенгуру не является млекопитающим» (Е) ложно. Подпротивные суждения (I и О) не могут быть одновременно ложными. Так, если суждение «Некоторые металлы не являются электропроводными» (О) ложно, то суждение «Некоторые металлы являются электропроводными» (I) (т. е. «Существуют металлы, которые электропроводны») является истинным. Подпротивные суждения могут оказаться и оба истинными. Таковы суждения «Некоторые металлы являются твердыми» (O)

и «Некоторые металлы не являются твердыми» (О).

Суждения, находящиеся в отношении подчинения (A, I и Е, О), отличаются, напр., тем важным свойством, что при истинности общих суждений соответствующие им частные также являются истинными. Так, истинность суждения «Все газы являются сжимаемыми» (A) влечет истинность подчиненного ему суждения (I) «Некоторые газы являются сжимаемыми».

ЛОГИЧЕСКИЙ ПОЗИТИВИЗМ - основное направление неопозитивизма. Возникло в 20-х годах XX в. под влиянием идей австрийского философа Л. Витгенштейна, который в своем главном произведении раннего периода «Логико-философский трактат» (1921 г., русский перевод 1958 г.) опирался на логическую систему, построенную Б. Расселом и А. Уайтхедом. В исчислении высказываний у нас имеется набор атомарных предложений, обладающих следующими свойствами: 1) каждое атомарное предложение является либо истинным, либо ложным; 2) атомарные предложения независимы друг от друга, т. е. истинность или ложность одного из них никак не влияет на истинность или ложность других атомарных предложений. Из атомарных предложений с помощью логических связок — отрицания, конъюнкции, дизъюнкции, импликации и т. п. — можно строить более сложные, молекулярные предложения, которые, в свою очередь, с помощью тех же связок можно объединять в еще более сложные предложения и т. д. Так возникает иерархия все более сложных молекулярных предложений.

В «Логико-философском трактате» Витгенштейн онтологизирует эту логическую структуру: он представляет мир как совокупность атомарных и молекулярных фактов, построенную точно также, как строится язык исчисления высказываний. Атомарные факты никак не связаны друг с другом, поэтому в мире нет никаких закономерных связей. Если действительность представляет собой лишь комбинации фактов, то наука должна быть комбинацией предложений, отображающих факты и их различные сочетания. Все, что претендует на выход за пределы этого «одномерного» мира фактов, все, что апеллирует к связи фактов или к глубинным сущностям, должно быть изгнано из науки как ненаучная, бессмысленная болтовня. Средством очищения науки от бессмысленных предложений является логический анализ языка науки.

Представители Л. п. развили эти идеи Витгенштейна в гносеологическом направлении. Их теория познания опиралась на следующие принципы.

1. Всякое знание есть знание о том, что дано человеку в чувственном восприятии.

2. То, что дано нам в чувственном восприятии, мы можем знать с абсолютной достоверностью.

3. Все функции знания сводятся к описанию.

Из этих основных принципов теории познания Л. п. вытекают некоторые другие его особенности. Сюда относится прежде всего отрицание традиционной философии, или «метафизики». Философия всегда стремилась сказать что-то о том, что лежит за ощущениями, стремилась вырваться из узкого круга субъективных переживаний.

Логический позитивист либо отрицает существование мира вне чувственных переживаний, либо считает, что о нем ничего нельзя сказать. В обоих случаях философия оказывается ненужной. Единственное, в чем она может быть хоть сколько-нибудь полезна, — это анализ научных высказываний. Поэтому философия отождествляется с логическим анализом языка. С отрицанием философии тесно связана терпимость Л. п. к религии. Если все разговоры о том, что представляет собой мир, объявлены бессмысленными, а вы тем не менее хотите говорить об этом, то безразлично, считаете ли вы мир идеальным или материальным, видите в нем воплощение Бога или населяете его демонами, — все это в равной степени не имеет к науке никакого отношения, а является сугубо личным делом каждого.

В основе науки, по мнению логических позитивистов, лежат протокольные предложения, выражающие чувственные переживания субъекта. Истинность этих предложений абсолютно достоверна и несомненна. Совокупность истинных протокольных предложений образует твердый эмпирический базис науки. Для методологии Л. п. характерно резкое разграничение эмпирического и теоретического уровней знания. Однако первоначально логические позитивисты полагали, что все предложения науки — подобно протокольным предложениям— говорят о чувственно данном. Поэтому каждое научное предложение можно свести к протокольным предложениям, подобно тому как любое молекулярное предложение экстенсиональной логики может быть разложено на составляющие его атомарные предложения. Достоверность протокольных предложений передается всем научным предложениям, поэтому наука состоит только из достоверно истинных предложений.

С точки зрения Л. п., деятельность ученого в основном должна сводиться к двум процедурам: 1) установление протокольных предложений; 2) изобретение способов объединения и обобщения этих предложений. Научная теория мыслилась в виде пирамиды, в вершине которой находятся основные понятия, определения и аксиомы; ниже располагаются предложения, выводимые из аксиом; вся пирамида опирается на совокупность протокольных предложений, обобщением которых она является. Прогресс науки выражается в построении таких пирамид и в последующем слиянии небольших пирамидок, построенных в некоторой конкретной области науки, в более крупные пирамиды, которые, в свою очередь, сливаются в еще более крупные и т. д. до тех пор, пока все научные теории и области не сольются в одну громадную систему — единую унифицированную науку. В этой примитивно-кумулятивной модели развития не происходит никаких потерь или отступлений: каждое установленное протокольное предложение навечно ложится в фундамент науки; если некоторое предложение обосновано с помощью протокольных предложений, то оно прочно занимает свое место в пирамиде научного знания.

Методологическая концепция Л. п. столкнулась с необходимостью решать многочисленные проблемы, вставшие перед ней в связи с той моделью науки, которую она сконструировала. Попытки решить первоначальные проблемы породили новые проблемы, а решение последующих проблем натолкнулось на новые трудности, и в конце концов методология Л. п. развалилась под грузом тех проблем и трудностей, которые она же и породила. Для сопоставления ее с реальной историей научного познания дело так и не дошло.

Вместе с тем последующее развитие философии науки существенно опиралось на те — как положительные, так и отрицательные — результаты, которые были получены Л. п. в его анализе структуры научного знания, языка науки, различных видов высказываний, входящих в науч