Методические рекомендации к проведению расчетов. Для того чтобы определить режим движения жидкости, необходимо рассчитать число Рейнольдса Re по формуле (4.3) для труб круглого сечения и по формуле (4.4) для
Для того чтобы определить режим движения жидкости, необходимо рассчитать число Рейнольдса Re по формуле (4.3) для труб круглого сечения и по формуле (4.4) для трубы произвольного сечения. В последнем случае гидравлический радиус рассчитывается по формуле (4.1) (пример 4.1). Затем сравнить полученное значение Re c критическим Re кр=2320 (пример 4.2). Значение критической скорости определяется по формуле (4.5), а соответствующий ей расход по формуле (4.2).
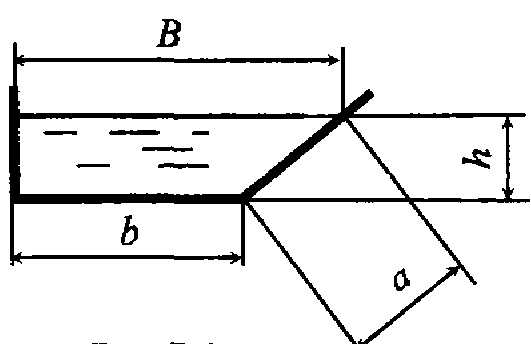
Задачи Задача 4.1. Жидкость движется в лотке со скоростью V = 0, 1 м/с. Глубина наполнения лотка h = 30 см, ширина по верху В = 50 см, ширина по низу b = 20 см. Определить смоченный периметр, площадь живого сечения, гидравлический радиус, расход, режим движения жидкости, если динамический коэффициент вязкости жидкости μ = 0, 0015 Па·с, а ее плотность ρ = 1200 кг/м3.
Задача 4.2. Найти минимальный диаметр d напорного трубопровода, при котором нефть будет двигаться при турбулентном режиме, если кинематический коэффициент вязкости нефти ν = 0, 3 см2/с, а расход в трубопроводе Q = 8 л/с. Задача 4.3. По трубе диаметром d = 0, 1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C. Задача 4.4. Определить критическую скорость, при которой происходит переход от ламинарного режима к турбулентному, в трубопроводе диаметром d = 30 мм при движении воды (ν = 0, 009 Ст), воздуха (ν = 0, 162 Ст) и глицерина (ν = 4, 1 Ст). Задача 4.5. Определить, изменится ли режим движения воды в напорном трубопроводе d = 0, 5 м при возрастании температуры от 15 до 65°С, если расход в трубопроводе Q = 15 л/с.
Задача 4.7. По трубе диаметром d = 0, 1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C.
Задача 4.9. Жидкость, имеющая динамический коэффициент вязкости μ = 1, 005 Па·с и плотность ρ = 900 кг/м3, движется в трапецеидальном лотке. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости. Глубина наполнения h = 0, 2 м, ширина лотка по дну b = 25 см, угол наклона боковых стенок лотка к горизонту α = 30°.
Задача 4.10. Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d = 12 мм и максимальный диаметр d = 3500 мм. Расчетные скорости движения воды в них V = 0, 5÷ 4 м/с. Определить минимальное и максимальное значение чисел Рейнольдса и режим течения в этих трубопроводах. Задача 4.11. Для осветления сточных вод используют горизонтальный отстойник, представляющий собой удлиненный прямоугольный резервуар. Его глубина h = 2, 6 м, ширина b = 5, 9 м. Температура воды t = 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расход Q = 0, 08 м3/с, а коэффициент кинематической вязкости ν = 1, 2·10-6 м2/с. При какой скорости в отстойнике будет наблюдаться ламинарный режим движения жидкости?
Задача 4.14. Определить режим движения воды при t = 20°С в смесителе, проходное сечение которого открыто наполовину, если d = 10 мм, расход воды Q = 0, 1 л/с.
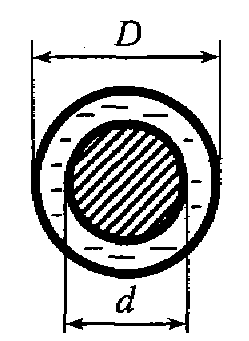
Задача 4.15. Смазка протекает через кольцевую щель. Определить гидравлический радиус при условии, что D = 50 мм, d = 48 мм. Задача 4.16. Определить гидравлический радиус для формы потока, изображенной на рисунке.
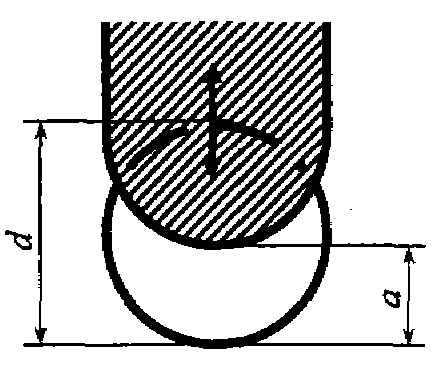
Задача 4.17. Определить гидравлический радиус, если простая задвижка на трубе круглого сечения d частично закрыта,
Задача 4.18. Построить эпюру скоростей и касательных напряжений в сечении трубы диаметром d = 50 мм, если расход потока Q = 100 см3/с, а температура воды t = 8°С. Задача 4.19. Определить максимальную и среднюю в сечении скорости, построить эпюру скоростей потока нефти в трубе диаметром d = 400 мм, если расход потока Q = 15 л/с, коэффициент кинематической вязкости ν = 0, 29 см2/с. Задача 4.20. Построить эпюру осредненных скоростей в сечении трубы, по которой протекает поток бензина с расходом Q = 60 л/с, если диаметр трубы d = 350 мм, кинематический коэффициент вязкости ν = 0, 0093 Ст. Гидравлический коэффициент трения λ = 0, 03. Контрольные вопросы и задания 1. Назовите основные параметры движущейся жидкости. 2. Перечислите основные виды движения. Приведите примеры. 2. Что такое площадь живого сечения потока, смоченный периметр и гидравлический радиус? 3. Напишите и объясните уравнение неразрывности потока. 4. Дайте определение ламинарного режима движения жидкости. 5. Охарактеризуйте турбулентный режим течения жидкости. 6. Что называется критической скоростью движения жидкости в трубе? 7. Изобразите схематически профили скоростей при ламинарном и турбулентном режимах течения жидкости в трубах. 8. Напишите формулу соотношения между средней и максимальной скоростью при ламинарном режиме. 9. Что такое осредненная местная скорость?
|

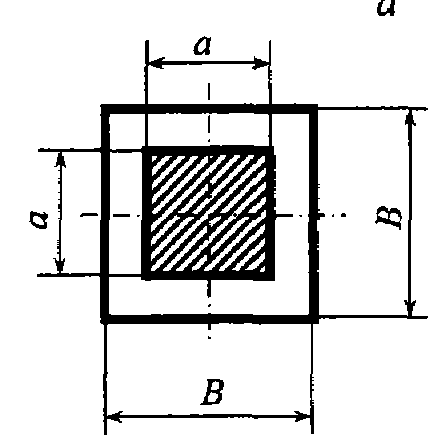
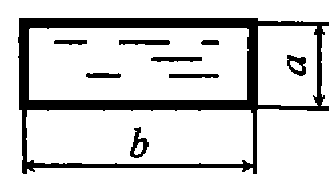 Задача 4.6. Вода движется под напором в трубопроводе прямоугольного сечения. Определить при каком максимальном расходе сохранится ламинарный режим. Температура воды t = 30°C, а = 0, 2 м, b = 0, 3 м.
Задача 4.6. Вода движется под напором в трубопроводе прямоугольного сечения. Определить при каком максимальном расходе сохранится ламинарный режим. Температура воды t = 30°C, а = 0, 2 м, b = 0, 3 м.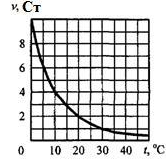 Задача 4.8. Жидкость движется в безнапорном трубопроводе с расходом Q = 22 м3/ч. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 80 мм. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости представлен на рисунке.
Задача 4.8. Жидкость движется в безнапорном трубопроводе с расходом Q = 22 м3/ч. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 80 мм. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости представлен на рисунке.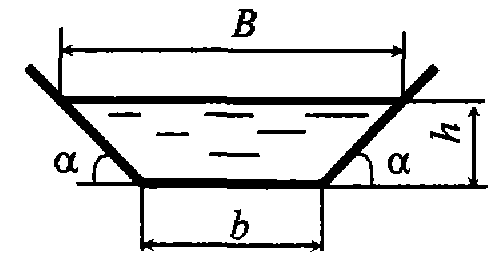
 Задача 4.12. Конденсатор паровой турбины оборудован 8186 трубками диаметром d = 2, 5 см. Через трубки пропускается охлаждающая вода при t = 10°С. Будет ли при расходе воды Q = 13600 м3/с обеспечен турбулентный режим движения в трубках?
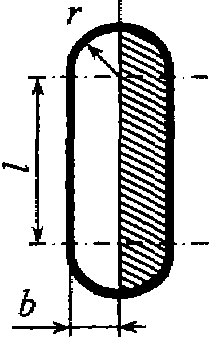
Задача 4.12. Конденсатор паровой турбины оборудован 8186 трубками диаметром d = 2, 5 см. Через трубки пропускается охлаждающая вода при t = 10°С. Будет ли при расходе воды Q = 13600 м3/с обеспечен турбулентный режим движения в трубках?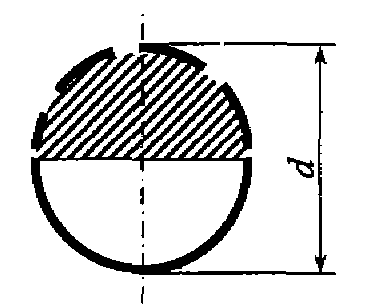 Задача 4.13. Определить режим движения горячей воды (t = 80°С) в пробковом кране, проходное сечение которого при частичном открытии изображено на рисунке, если l = 20 мм, b = r = 3 мм, расход воды Q = 0, 1 л/с.
Задача 4.13. Определить режим движения горячей воды (t = 80°С) в пробковом кране, проходное сечение которого при частичном открытии изображено на рисунке, если l = 20 мм, b = r = 3 мм, расход воды Q = 0, 1 л/с.