Гидравлический расчет трубопроводов
Все трубопроводы подразделяются на две категории: простые и сложные. Простой трубопровод не имеет разветвлений на пути движения жидкости, но может представлять последовательное соединение труб разного диаметра. Сложный трубопровод имеет хотя бы одно разветвление и может содержать как параллельные и последовательные соединения труб. Если в трубопроводе необходимо обеспечить расход жидкости Q, то потребный для этого напор Н потр. – пьезометрическая высота в начальном сечении определяется по формуле
где Суммарная потеря напора складывается из потерь на трение по всей длине трубы и местных потерь
Для определения потерь напора на трение в трубах круглого сечения можно использовать формулу Дарси, которую для дальнейших расчетов удобно выразить через расход:
где l – длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси). При турбулентном движении коэффициент трениязависит от числа Рейнольдса Универсальной формулой, учитывающей одновременно оба фактора является формула Альтшуля:
Для гидравлически гладких труб шероховатость на сопротивление не влияет, и коэффициент сопротивления
Местные потери напора определяются по формуле Вейсбаха:
где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами). C учетом формул Дарси и Вейсбаха,
При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):
Обозначим В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен
где S1 и S 2 – площади сечений трубы до и после сужения. Формула (6.6) справедлива для обоих режимов, однако для ламинарного режима удобнее использовать формулу Пуазейля:
в которой необходимо заменить фактическую длину трубопровода расчетной, равной
где Формула для расчета потребного напора имеет вид
где для ламинарного режима течения
турбулентного режима течения
Характеристики потребного напора
|

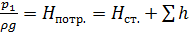 , (6.1)
, (6.1) – статический напор,
– статический напор,  - суммарные потери напора на сопротивление в трубопроводе.
- суммарные потери напора на сопротивление в трубопроводе. +
+ 
 (6.2)
(6.2) и относительной шероховатости трубы ε
и относительной шероховатости трубы ε  Значения эквивалентной (абсолютной) шероховатости Δ для различных труб представлены в Приложении 7.
Значения эквивалентной (абсолютной) шероховатости Δ для различных труб представлены в Приложении 7. (6.3)
(6.3) однозначно определяется числом Рейнольдса:
однозначно определяется числом Рейнольдса: (6.4)
(6.4) (6.5)
(6.5) (6.6)
(6.6)
 - коэффициент местных сопротивлений при расширении трубы, где d1 и d 2 – внутренние диаметры сечений трубы перед и за расширением.
- коэффициент местных сопротивлений при расширении трубы, где d1 и d 2 – внутренние диаметры сечений трубы перед и за расширением. ,
,
 , (6.7)
, (6.7) ,
, – длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе.
– длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе. , (6.8)
, (6.8) , m =1; (6.9)
, m =1; (6.9) , m =2 (6.10)
, m =2 (6.10) и суммарных потерь напора трубопроводов
и суммарных потерь напора трубопроводов  при ламинарном режиме представляет прямые, при турбулентном - параболы.
при ламинарном режиме представляет прямые, при турбулентном - параболы.


