Методические рекомендации к проведению расчетов. Для решения задачи с применением уравнения Бернулли следует:

Для решения задачи с применением уравнения Бернулли следует:

1) выбрать два сечения, для которых записывается уравнение. В качестве сечений рекомендуется брать:

- выход в атмосферу, где _абс = р_а;

- свободную поверхность в резервуаре, где скорость V = 0

- сечение, в котором присоединен прибор для измерения давления (манометр, вакуумметр, пьезометр и др.).

2) записать уравнение Бернулли в общем виде – формула (5.1) для идеальной жидкости и формула (5.2) для реальной жидкости;

3) переписать уравнение для заданных сечений с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

При этом необходимо помнить:

- уравнение Бернулли записывается по течению жидкости;

- вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;

- давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);

- коэффициент Кориолиса в задачах на движение потока реальной жидкости следует учитывать только при ламинарном режиме течения α = 2, для турбулентных потоков можно принимать α = 1;

- суммарная потеря напора записывается в правой части уравнения со знаком «+» и складывается из местных потерь, которые определяются формулой Вейсбаха, и потерь на трение по длине, определяемых формулой Дарси.

 

Задачи

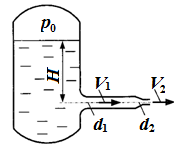Задача 5.1. Из напорного бака вода течет по трубе диаметром d ₁ = 20 мм и затем вытекает в атмосферу через брандспойт с диаметром выходного отверстия d ₂ = 10 мм. Избыточное давление воздуха в баке р ₀ = 0, 18 МПа; высота Н = 1, 6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V ₁ и на выходе

из насадка V ₂.

Задача 5.2. Определить скорость движения бензина V и расход Q в сифонном трубопроводе. Нижняя точка оси трубопровода расположена ниже уровня жидкости в питающем резервуаре на расстоянии h = 2, 5 м. Внутренний диаметр трубопровода d = 25 мм, плотность бензина ρ = 850 кг/м³. Потерями напора пренебречь.

Задача 5.3. Определить расход жидкости Ж, вытекающей из бака по трубопроводу диаметром d, если избыточное давление воздуха в баке р ₀, высота уровня Н ₀, высота подъема жидкости в пьезометре, открытом в атмосферу Н. Потерями энергии пренебречь.

Задача 5.4. Вода движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление больше в сечении 1-1 Δ р = 25 кПа. Определить расход Q, если внутренний диаметр трубопровода в сечении 1-1 D = 65 мм, а в сечении 2-2 d = 40 мм, разность отметок сечений Δ z = 2 м. Потерями напора пренебречь.

Задача 5.5. Керосин движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление в сечении 1-1 р ₁ = 35 кПа. Определить избыточное давление в сечении 2-2, если внутренний диаметр трубопровода в сечении 1-1 D = 50 мм, а в сечении 2-2 d = 35 мм, разность отметок сечений Δ z = 1 м, расход Q = 2 л/с. Потерями напора пренебречь.

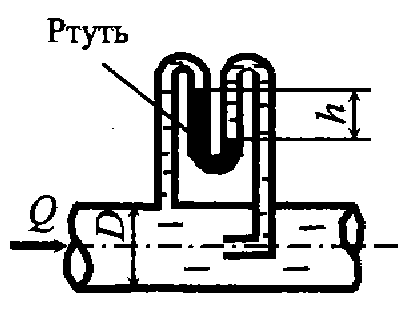Задача 5.6. Определить расход воды в трубопроводе, если согласно показаниям ртутного дифференциального манометра h = 30 мм. Плотность ртути ρ = 13600 кг/м³, внутренний диаметр трубопровода D = 80 мм. Потери напора не учитывать.

Задача 5.7. По горизонтальной трубе переменного сечения протекает нефть с расходом Q = 1, 3 л/с. Определить разность показаний пьезометров h, если диаметр трубопровода в широком сечении D = 10 см, а в узком d = 5 см. Плотность нефти ρ = 850 кг/м³. Потерями напора пренебречь.

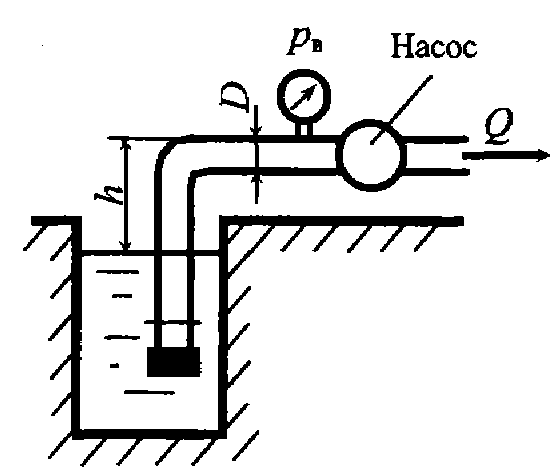Задача 5.8. Насос с подачей Q = 7, 2 м³/ч забирает воду из колодца. Определить наибольший вакуум p _вак при входе в насос. Внутренний диаметр трубопровода D = 80 мм, высота установки насоса над уровнем жидкости h = 4 м. Потери напора Δ h = 0, 5 м.

Задача 5.9. По трубопроводу диаметром D = 150 мм движется вода с расходом 20 л/мин. Определить, пренебрегая потерями напора, разность уровней в жидкостном манометре. Плотность жидкости в манометре ρ = 1300 кг/м³.

Задача 5.10. Нефть движется под напором в трубопроводе квадратного сечения. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости, если сторона квадрата a = 0, 05 м, динамический коэффициент вязкости μ = 0, 02 Па·с, а плотность нефти ρ = 850 кг/м³.

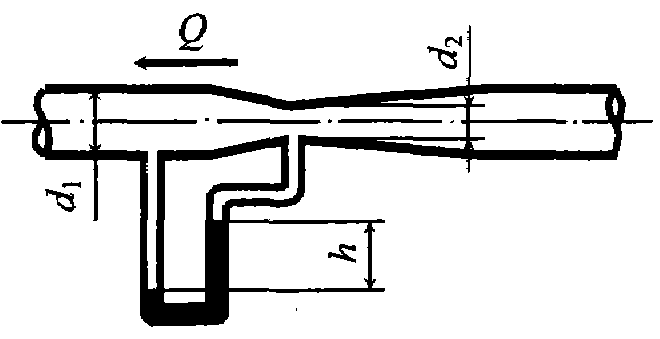Задача 5.11. По горизонтальному трубопроводу переменного сечения движется нефть, плотность которой ρ = 850 кг/м³. Диаметр в широком сечении трубопровода d ₁ =50 мм. Расход жидкости в трубопроводе Q = 0, 5 л/с, разность уровней в дифференциальном манометре, заполненном ртутью плотностью ρ = 13600кг/м³, составляет h = 35 мм. Определить диаметр трубопровода в узком сечении. Потерями напора пренебречь.

Задача 5.12. Определить скорость и расход газа с плотностью ρ = 20 кг/м³ в трубопроводе с внутренним диаметром D = 50 мм. В колене манометра находится жидкость плотностью ρ _ж = 1000 кг/м³. Потери напора не учитывать.

Задача 5.13. По горизонтальному трубопроводу переменного сечения движется вода. Из бачка А по трубке, подведенной к трубопроводу, поступает краситель, имеющий плотность ρ = 1300 кг/м³. Определить расход воды в трубопроводе, при котором прекратится подача красителя. Уровень красителя в 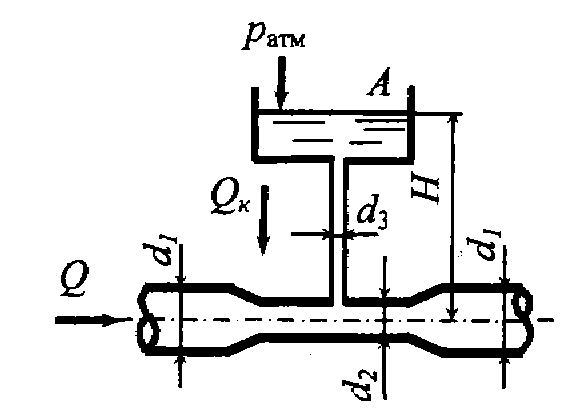бачке H = 0, 5 м, диаметр трубопровода в широком сечении d ₁ = 150 мм, в узком – d ₂ = 100 мм, избыточное давление воды в широком сечении трубопровода составляет 30 кПа. Потерями напора пренебречь.

Задача 5.14. Для условий задачи 4.13 определить, при какой высоте Н прекратится подача красителя. Расход воды в трубопроводе Q = 1, 8 м³/мин, диаметр трубопровода в широком сечении d ₁ = 200 мм, в узком – d ₂ = 100 мм, абсолютное давление воды в широком сечении трубопровода составляет 150 кПа. Потерями напора пренебречь.

Задача 5.15. Определить давление в сечении трубопровода с диаметром d ₁ = 0, 1 м, если вода в трубке поднялась на высоту h = 3 м, диаметр cуженой части трубопровода d ₂ = 0, 6 м, расход воды в трубопроводе Q = 0, 0065 л/с. Потери напора не учитывать.

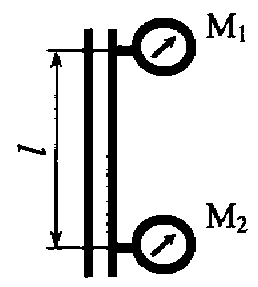Задача 5.16. На вертикальной водопроводной трубе постоянного диаметра на расстоянии l = 10 м установлены два манометра. Нижний манометр показывает давление 1, 2 кг/см², а верхний – 0, 8 кг/см². Определить гидравлический уклон и направление движения жидкости.

Задача 5.17. По нагнетательному патрубку диаметром d ₁ = 200 мм вентилятором подается воздух плотностью ρ = 1, 2 кг/м³ с расходом Q = 0, 8 м³/с при избыточном давлении р ₁ = 1 кПа. К патрубку подсоединен диффузор с диаметром выходного сечения d ₂ = 300 мм. Определить давление воздуха на выходе из диффузора. Изменение плотности воздуха и потери в диффузоре не учитывать.

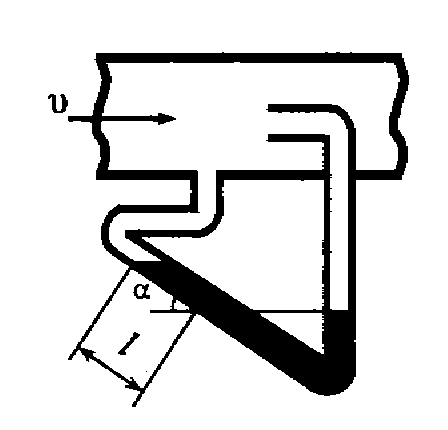Задача 5.18. К трубе, по которой движутся дымовые газы плотностью ρ = 0, 6 кг/м³, присоединен микроманометр, заполненный спиртом (ρ _сп = 0, 6 кг/м³). Показание шкалы манометра, наклоненной под углом α = 30° к горизонту, l = 15 мм. Определить скорость движения дымовых газов.

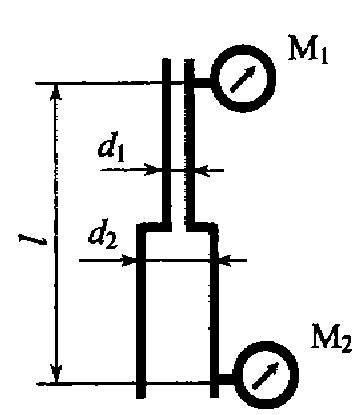Задача 5.19. На вертикальной водопроводной трубе, состоящей из труб диаметром d ₁ = 27 мм и d ₂ = 15 мм, установлены два манометра. Нижний манометр показывает давление 1, 6 кг/см², а верхний – 1, 2 кг/см². Определить направление движения воды, гидравлический и пьезометрический уклоны, если расход составляет Q = 0, 3 л/с.

Задача 5.20. Поршень диаметром D = 200 мм вытесняет воду по короткому трубопроводу диаметром d = 20 мм в атмосферу. Определить усилие на поршень, если скорость истечения жидкости v = 5 м/с, потери напора h _w = 2 м.

 

Контрольные вопросы и задания

1. Напишите уравнение Бернулли для элементарной струйки движущейся жидкости и объясните, какие параметры оно связывает.

2. Объясните геометрический и энергетический смысл уравнения Бернулли?

3. Чем отличается уравнение Бернулли для потока реальной жидкости от уравнения, составленного для элементарной струйки идеальной жидкости?

4. Чем обусловлены потери напора в потоке реальной жидкости?

5. Что такое гидродинамический напор? Чему он равен?

6. От чего зависит скоростной напор и чему он равен?