Методические рекомендации к проведению расчетов
Для того, чтобы определить силу суммарного давления на плоскую стенку следует: 1) определить глубину погружения центра тяжести стенки 2) найти площадь смачиваемой поверхности стенки S; 3) рассчитать суммарную силу давления по формуле (3.1); 4) точку приложения силы давления – центр давления – определить по формуле (3.2), где момент инерции рассчитывается по формулам, приведенным в приложении 5 (см. примеры 3.1 и 3.2)
Для того, чтобы определить силу суммарного давления на криволинейную стенку следует: 1) определить горизонтальную и вертикальную составляющие по формулам (3.4) и (3.5); 2) вычислить суммарную силу давления, используя формулу (3.3); 3) направление силы давления показать, определив угол β по формуле (3.6) (см. пример 3.1).
Для построения эпюр давления – диаграмм распределения давления на смоченную поверхность следует: 1) в точке соприкосновения свободной поверхности жидкости со стенкой восстанавливают перпендикуляр и на нем откладывают значение давления р 0; 2) из точки пересечения стенки со дном восстанавливают другой перпендикуляр, равный в масштабе сумме значений р 0 и ρ gH; 3) соединив полученные отрезки, получают эпюру абсолютного давления. Задачи
Задача 3.6. Определить равнодействующую силу и центр давления воды на прямоугольную стенку шириной b = 10 м, если глубина воды Н 1=5 м, Н 2=3 м.
Задача 3.7. В вертикальной стенке имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 1, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 2, 3 м.
Задача 3.8. В вертикальной стенке имеется отверстие, перекрываемое щитом в форме эллипса с размерами а = 1, 5 м, b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 0, 3 м.
Задача 3.12. Построить тело давления и определить силу, открывающую полусферическую крышку диаметром d = 1 м, Н = 2 м. Задача 3.13. Построить тело давления и определить силу, прижимающую коническую крышку диаметром d = 1, 2 м к основанию резервуара. Резервуар заполнен водой, глубина воды Н = 3 м, высота крышки h = 1 м.
Задача 3.14. Определить величину и направление силы давления воды на боковую поверхность цилиндрического затвора диаметром d = 1, 6 м и длиной l = 4 м. Глубина воды Н = 3 м.
Контрольные вопросы и задания 1. Как определить силу гидростатического давления на плоскую стенку? 2. К какой точке приложена эта сила? 3. В чем смысл гидростатического парадокса? 4. Как найти силу гидростатического давления и точку ее приложения, если стенка цилиндрическая? 5. Что называется телом давления? 6. Как определить направление силы суммарного давления на цилиндрические поверхности? Основные понятия гидродинамики Гидродинамика - раздел гидравлики, изучающий законы движения жидкости и их практическое применение. Движение жидкости может быть установившимся и неустановившимся, равномерным и неравномерным, напорным и безнапорным. При неустановившемся движении скорость и давление в выбранной точке пространства зависит от координат и изменяется с течением времени. При установившемся движении его характеристики не изменяются с течением времени и зависят только от координат рассматриваемой точки. При напорном движении потокжидкости со всех сторон ограничен твердыми стенками (закрытое русло), а давление отличается от атмосферного; При безнапорном движении – поток имеет свободную поверхность, давление над которой атмосферное. При изучении движущейся жидкости вводится ряд понятий, характеризующих гидравлические и геометрические элементы потока. Живым сечением называют поверхность потока, проведенная перпендикулярно к направлению линий тока. Живое сечение характеризуется площадью живого сечения ω (м²), смоченным периметром χ (м) и гидравлическим радиусом R (м). Смоченный периметр χ – длина части периметра живого сечения, по которой поток соприкасается с ограничивающими его стенками. Отношение площади живого сечения потока к смоченному периметру называется гидравлическим радиусом:
В приложении 6 приведены значения гидравлических радиусов для потоков разных сечений. Расходом жидкости называется количество жидкости, протекающей через живое сечение потока за единицу времени. Различают: - объемный Здесь - массовый M, кг/с; - весовой G, Н/с. При установившемся движении расход жидкости для любого сечения есть величина постоянная. Q = Выражение (4.1) представляет уравнение неразрывности потока.
Многочисленные экспериментальные исследования движущихся жидкостей позволили установить существование двух режимов движения жидкости: ламинарного и турбулентного. При ламинарном режиме движения, наблюдаемом при малых скоростях, отдельные струйки жидкости движутся параллельно друг другу. При турбулентном режиме наблюдается сильное перемешивание частиц жидкости и как следствие неупорядоченное движение ее элементов. Скорость, при которой происходит смена режимов, называется критической. Для характеристики режима движения жидкости введен безразмерный параметр – число Рейнольдса, которое для труб круглого сечения выражают через внутренний диаметр трубопровода:
Для потока произвольной формы число Рейнольдса выражается через гидравлический радиус
Минимальное значение, соответствующее переходу ламинарного режима в турбулентный определяется критическим числом Рейнольдса Reкр.=2320 или Следовательно, значение критической скорости:
При ламинарном режиме движения в цилиндрической трубе радиусом r 0 распределение местных скоростей подчиняется параболическому закону. Максимальная скорость имеет место на оси трубопровода, тогда местная скорость в слое жидкости, находящемся на расстоянии r от оси трубы
Средняя скорость Максимальная скорость
Касательная напряжения у стенки трубы
Касательные напряжения по сечению трубы распределяются по зависимости
При турбулентном режиме движения распределение осредненных скоростей
где y – расстояние от стенки трубы до рассматриваемой точки;
Максимальная скорость связана со средней скоростью в сечении следующей зависимостью
|

 (используя приложение 5);
(используя приложение 5); Задача 3.1. Определить силу гидростатического давления и центр давления воды на прямоугольный затвор шириной b = 1, 2 м, закрывающий вход в прямоугольную трубу, высота которой h = 0, 8 м. Глубина жидкости в резервуаре H = 3, 5 м, а = 0, 5 м.
Задача 3.1. Определить силу гидростатического давления и центр давления воды на прямоугольный затвор шириной b = 1, 2 м, закрывающий вход в прямоугольную трубу, высота которой h = 0, 8 м. Глубина жидкости в резервуаре H = 3, 5 м, а = 0, 5 м.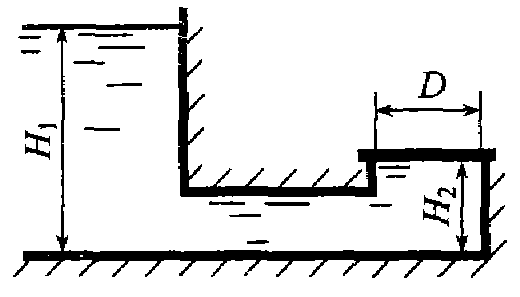 Задача 3.2. Определить силу гидростатического давления жидкости на круглую крышку колодца диаметром D = 1, 2 м. Относительная плотность жидкости δ = 1, 25, глубины H 1 = 4, 5 м, H 2 = 1, 0 м.
Задача 3.2. Определить силу гидростатического давления жидкости на круглую крышку колодца диаметром D = 1, 2 м. Относительная плотность жидкости δ = 1, 25, глубины H 1 = 4, 5 м, H 2 = 1, 0 м. Задача 3.3. Определить силу и центр давления воды на стенку шириной b = 15 м, глубина воды h = 3 м.
Задача 3.3. Определить силу и центр давления воды на стенку шириной b = 15 м, глубина воды h = 3 м.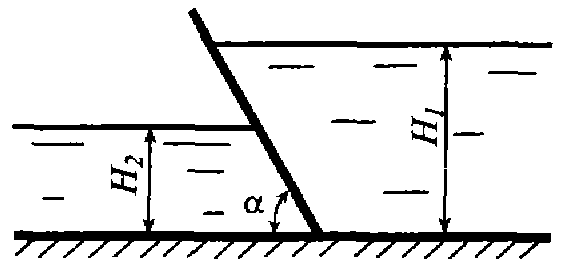 Задача 3.4. Определить равнодействующую силу и центр давления воды на наклонную прямоугольную стенку шириной b = 10 м, если глубина воды Н 1 = 6 м, Н 2 = 2 м, а угол наклона стенки α = 60°.
Задача 3.4. Определить равнодействующую силу и центр давления воды на наклонную прямоугольную стенку шириной b = 10 м, если глубина воды Н 1 = 6 м, Н 2 = 2 м, а угол наклона стенки α = 60°. Задача 3.5. Прямоугольное отверстие высотой h = 0, 4 м и шириной b = 1 м в вертикальной стенке открытого резервуара с водой закрыто щитом. Определить силу и центр давления воды на щит, если Н = 1, 3 м.
Задача 3.5. Прямоугольное отверстие высотой h = 0, 4 м и шириной b = 1 м в вертикальной стенке открытого резервуара с водой закрыто щитом. Определить силу и центр давления воды на щит, если Н = 1, 3 м.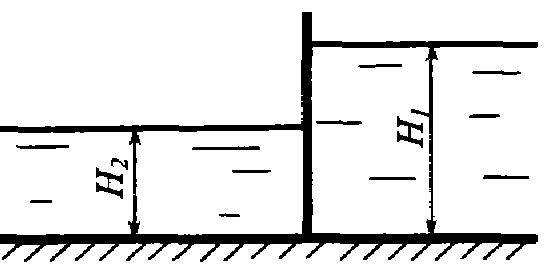


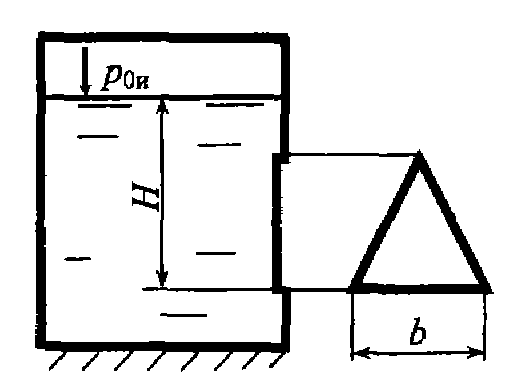 Задача 3.9. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается равносторонним треугольным щитом со стороной b = 1, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 2, 3 м, избыточное давление в резервуаре р 0изб = 5 кПа.
Задача 3.9. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается равносторонним треугольным щитом со стороной b = 1, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 2, 3 м, избыточное давление в резервуаре р 0изб = 5 кПа. Задача 3.10. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1, 5 м, b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 3, 2 м, вакуумметрическое давление в резервуаре р 0вак = 10 кПа.
Задача 3.10. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1, 5 м, b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 3, 2 м, вакуумметрическое давление в резервуаре р 0вак = 10 кПа.
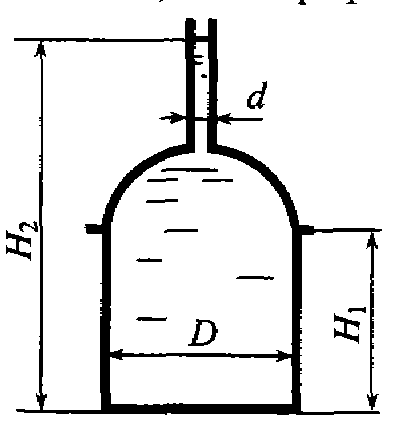 Задача 3.11. Цилиндрический резервуар для хранения мазута диаметром D = 4 м имеем полусферическую крышку и сообщается с атмосферой через трубу диаметром d = 0, 2 м. Определить вертикальную составляющую силы гидростатического давления мазута на крышку, если Н 1 = 4 м, Н 2 = 8 м, а плотность мазута ρ = 890 кг/м3.
Задача 3.11. Цилиндрический резервуар для хранения мазута диаметром D = 4 м имеем полусферическую крышку и сообщается с атмосферой через трубу диаметром d = 0, 2 м. Определить вертикальную составляющую силы гидростатического давления мазута на крышку, если Н 1 = 4 м, Н 2 = 8 м, а плотность мазута ρ = 890 кг/м3.

 Задача 3.15. Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 1, 25 на затвор. Затвор является частью цилиндра радиусом R = 2, 6 м, глубина жидкости в резервуаре Н = 3, 8 м.
Задача 3.15. Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 1, 25 на затвор. Затвор является частью цилиндра радиусом R = 2, 6 м, глубина жидкости в резервуаре Н = 3, 8 м.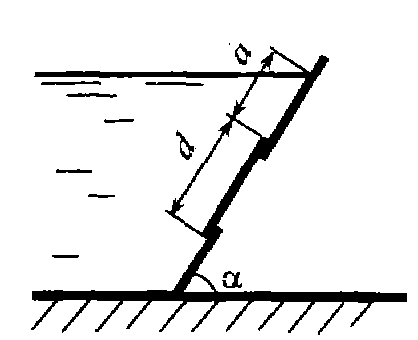 Задача 3.16. На щите, наклоненном к горизонту на угол α = 60°, имеется отверстие, которое перекрывается круглой крышкой диаметром d = 0, 8 м. Определить силу гидростатического давления и центр давления воды на крышку люка, а = 1, 0 м.
Задача 3.16. На щите, наклоненном к горизонту на угол α = 60°, имеется отверстие, которое перекрывается круглой крышкой диаметром d = 0, 8 м. Определить силу гидростатического давления и центр давления воды на крышку люка, а = 1, 0 м. Задача 3.17. В вертикальной стенке имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 3, 4 м.
Задача 3.17. В вертикальной стенке имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 3, 4 м.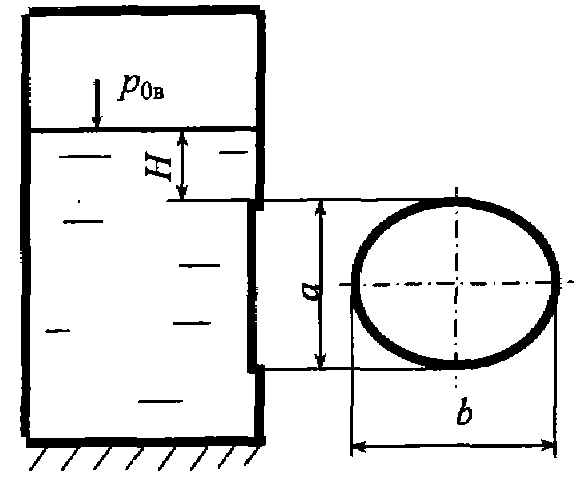 Задача 3.18. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1, 5 м, b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 0, 3 м, вакуумметрическое давление в резервуаре р 0вак = 20 кПа.
Задача 3.18. В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1, 5 м, b = 2, 5 м. Определить силу гидростатического давления и положение центра давления, если H = 0, 3 м, вакуумметрическое давление в резервуаре р 0вак = 20 кПа. Задача 3.19. Построить тело давления и определить силу, прижимающую полусферическую крышку диаметром d = 1, 2 м к основанию резервуара. Резервуар заполнен водой, глубина воды Н = 3 м.
Задача 3.19. Построить тело давления и определить силу, прижимающую полусферическую крышку диаметром d = 1, 2 м к основанию резервуара. Резервуар заполнен водой, глубина воды Н = 3 м. Задача 3.20. Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 0, 8, действующей на цилиндрическую поверхность, если радиус и длина образующей цилиндра соответственно R = 1, 2 м, b = 0, 5 м.
Задача 3.20. Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 0, 8, действующей на цилиндрическую поверхность, если радиус и длина образующей цилиндра соответственно R = 1, 2 м, b = 0, 5 м. (4.1)
(4.1) м3/с,
м3/с,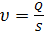 - средняя скорость потока в данном живом сечении - условная одинаковая во всех точках скорость, при которой расход потока будет такой же, как и при различных местных скоростях.
- средняя скорость потока в данном живом сечении - условная одинаковая во всех точках скорость, при которой расход потока будет такой же, как и при различных местных скоростях.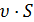 = сonst (4.2)
= сonst (4.2) (4.3)
(4.3)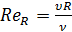 (4.4)
(4.4)
 (4.5)
(4.5)
 .
. =
= 

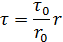
 по сечению трубы может быть приближенно принято по зависимости
по сечению трубы может быть приближенно принято по зависимости ,
, – динамическая скорость.
– динамическая скорость.



