Параллельные реакции
Согласно принципу независимости протекания реакции (I) и (II) к ним можно применить основной постулат химической кинетики:
Пусть Общая скорость параллельных реакций равна алгебраической сумме скоростей, т.е.:
В общем виде можно записать:
Интегрирование этого уравнение дает следующее соотношение: При любом Кинетические кривые параллельных реакции Совместное решение уравнений (2) и (3) позволяет найти отдельно К1 и К2. Графические зависимости концентраций веществ А, В, С от времени для параллельной реакции можно представить следующим образом, при K1> K2 (рисунок).
Рисунок – Кинетические кривые параллельной реакции
Сложные параллельные реакции
то кинетическое уравнение запишется: Чтобы найти каждую из констант скоростей в отдельности необходимо решить следующую систему уравнений:
В параллельных реакциях, включающих реакции одинакового порядка, выход продуктов определяется отношением их констант скоростей. Более сложным случаем является рассмотрение параллельных реакции разного порядка, входящих в состав одного процесса. Последовательные реакции Последовательными называются такие реакции, в которых продукт одной реакции является исходным веществом для другой. Кинетику последовательных реакций рассмотрим на примере следующей реакции: Каждая из этих реакций идет с определенной скоростью. Запишем изменение концентрации А, В, С во времени. Пусть при t=0 сА=с0, св=сС=0, а при t> 0 сА+ св+ сС= с0. Изменение концентрации (сА) во времени будет:
Скорость накопления и исчезновения вещества В будет:
Скорость накопления вещества С будет:
Из уравнения (1) легко найти, что Подставим значение сА в уравнение (2):
Решение этого уравнения позволяет найти функциональную зависимость концентрации промежуточного продукта:
Далее рассмотрим функциональную зависимость для продукта реакции: Концентрация сС=с0-сА-сВ, зная сА и сВ, найдем:
Кинетические кривые для последовательных реакции первого порядка Представим графическую зависимость изменения концентраций сА, св, сС от времени для реакции Как видно из данного рисунка, концентрация промежуточного продукта сВ проходит через максимум. В последовательных реакциях в начальный момент времени концентрация конечного продукта сС=0 и требуется время (индукционный период), чтобы сначала образовался промежуточный продукт В, а потом он переходит в С, т.е. сВ® сС. Максимальное накопление промежуточного продукта определяют, как первую производную концентрации промежуточного вещества:
Анализ уравнения (1) позволяет найти:
Рисунок – Зависимость концентрации исходного (1), промежуточного (2) и конечного продукта (3) от времени для последовательной односторонней реакции первого порядка
Из уравнения (2) следует, что tмах зависит от соотношения К2 к К1, т.е. закономерности протекания последовательных реакциях зависят от Время накопления промежуточного продукта в последовательной реакции а) при К1> > K2, скорость образования В больше, чем С, т.е.чем больше К1, тем больше концентрация промежуточного продукта (максимум на рисунке) и больше значение по оси абсцисс экстремальной точки (tмах) (рисунок, кривая 1). б) при K2> > К1 за более меньшее время достигается максимум концентрации промежуточного продукта, ее ордината меньше и смещена к оси ОУ (рисунок, кривая 2).
Рисунок – Зависимость концентрации промежуточного вещества от времени
Лекция 4
Квазистационарный режим последовательной реакции При рассмотрении закономерностей протекания последовательных реакций наиболее интересным и информативными условиями являются два крайних случая, когда K1> > К2 и K2> > К1. 1. При K1> > К2 скорость образования промежуточного вещества В в реакции Начиная с некоторого момента времени, несколько большего tmax, первым слагаемым в уравнении СВ =
Из уравнения (2) следует, что последовательная реакция при этих условиях будет протекать, как обычная реакция первого порядка. 2. При K2> > К1 в уравнении (1) можно пренебречь вторым слагаемым и тогда
В этом случае скорость превращения промежуточного вещества В в продукт С будет значительно выше скорости его возникновения из исходного вещества А, а его концентрация будет весьма низкой. Отношение СВ/СА из уравнений
Из уравнения (4) следует, что с течением времени отношение концентраций (СВ/СА) не изменяется. Эта ситуация подобна тому, когда реакция протекает в стационарных условиях, т.е. Таким образом, хотя при протекании последовательной реакции в закрытой системе и не может быть стационарного режима, но при некоторых условиях, когда K2> > К1 Такой режим протекания реакции называется квазистационарным, т.е. условно считается, что концентрация промежуточного продукта стационарна во времени,
Координата перегиба на кинетической кривой продукта в последовательной реакции На кривой накопления продукта реакции имеется перегиб, и tперегиб= tмах промежуточного продукта. Точка перегиба соответствует второй производной концентрации продукта реакции и она равна:
Решение уравнения (1) доказывает, что время перегиба соответствует времени максимального накопления промежуточного вещества. tперегиба=
Метод стационарных концентрации Боденштейна Способ приближенного решения прямой кинетической задачи, основанной на предположении о малости и постоянстве концентраций неустойчивых промежуточных продуктов, был предложен в 1913 г. М. Боденштейном и получил название метода стационарных концентраций или метода Боденштейна. Математически это записывается как: Таким образом, суть метода стационарных концентраций состоит в том, что он позволяет выразить концентрации неустойчивых частиц, количественное определение которых без специальной техники затруднено, через концентрации устойчивых составляющих в реакционной смеси путем составления системы уравнений изменений концентраций реактивов и реагирующих веществ.
|

 Параллельными называются такие реакции, когда исходные вещества одновременно участвуют в двух или нескольких реакциях с образованием разных продуктов реакции. Например, две параллельные реакции первого порядка:
Параллельными называются такие реакции, когда исходные вещества одновременно участвуют в двух или нескольких реакциях с образованием разных продуктов реакции. Например, две параллельные реакции первого порядка: и
и 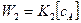
 при
при  . К моменту времени
. К моменту времени 
 , где х = хВ+хС.
, где х = хВ+хС.
 или
или 
 . Это уравнение также идентично уравнению необратимой реакции I порядка. Значение (а-х) для данной параллельной реакции может быть представлено как:
. Это уравнение также идентично уравнению необратимой реакции I порядка. Значение (а-х) для данной параллельной реакции может быть представлено как: 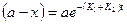 .
.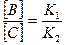 .
.
 Если идут три параллельные реакции первого порядка:
Если идут три параллельные реакции первого порядка: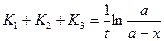 .
.

 .
. (1)
(1) (2)
(2) (3)
(3)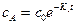 ;
;




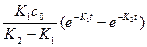 =
= 


 (1)
(1) или
или  =
=  , где
, где  (2)
(2)
 .
.
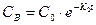 (2).
(2). (3)
(3) и СВ из уравнения (3) дает зависимость:
и СВ из уравнения (3) дает зависимость: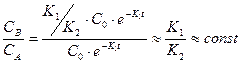 (4)
(4)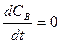 .
. .
. . Обычно это выполняется для реакций с участием радикалов и других активных частиц.
. Обычно это выполняется для реакций с участием радикалов и других активных частиц. (1)
(1) =
=  .
.


