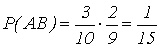Условная вероятность. Теорема умножения вероятностей
Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В. Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А). Таким образом, Р(A)=1/4; PB(А)=1/2 Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2,..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого. Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы. В случае независимости событий A к B формула (4) примет более простой вид:
События А1, А2,..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились. Исходя из этого определения, в случае независимости событий А1, А2,..., Аn между собой в совокупности на основании формулы (7) имеем
Пример 1. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз? Решение: Пусть событие Ai — появление герба при i -м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai(i=1, 2, 3,..., 10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем
Решение:
Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
|

 ;
;  ;
; 





 и
и 


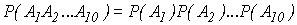



 , состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем
, состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем