Рассмотрим случайную величину *  , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2,..., xn,.... Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1, 2,...) равно вероятности того, что величина
, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2,..., xn,.... Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1, 2,...) равно вероятности того, что величина  примет значение xi
примет значение xi

| (16)
|
Такая случайная величина  называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2,..., xn,.... Так как в каждом из испытаний случайная величина
называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2,..., xn,.... Так как в каждом из испытаний случайная величина  принимает всегда какое-либо значение из области ее изменения, то
принимает всегда какое-либо значение из области ее изменения, то

Пример 1. Случайная величина  — число очков, выпадающих при однократном бросании игральной кости. Возможные значения
— число очков, выпадающих при однократном бросании игральной кости. Возможные значения  — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что
— числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что  примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения?
примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения?
Решение: Таким образом, здесь закон распределения вероятностей есть функция р(х)=1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.
Пример 2. Пусть случайная величина  - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений
- число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений  состоит из 2-х чисел 0 и 1:
состоит из 2-х чисел 0 и 1:  =0, если событие A не произошло, и
=0, если событие A не произошло, и  =1, если событие A произошло. Таким образом,
=1, если событие A произошло. Таким образом,

Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить событие A. Пусть вероятность наступления события A при каждом испытании равна p. Рассмотрим случайную величину  — число наступлений события A при n независимых испытаниях. Область изменения
— число наступлений события A при n независимых испытаниях. Область изменения  состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):
состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):

Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m -й член разложения бинома  .
.
Пусть случайная величина  может принимать любое целое неотрицательное значение, причем
может принимать любое целое неотрицательное значение, причем
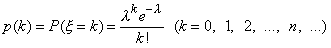
| (17)
|
где 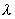 — некоторая положительная постоянная. В этом случае говорят, что случайная величина
— некоторая положительная постоянная. В этом случае говорят, что случайная величина  распределена по закону Пуассона, Заметим, что при k=0 следует положить 0! =1.
распределена по закону Пуассона, Заметим, что при k=0 следует положить 0! =1.
Как мы знаем, при больших значениях числа n независимых испытаний вероятность Pn(m) наступления m раз события A удобнее находить не по формуле Бернулли, а по формуле Лапласа [см. формулу (15)]. Однако последняя дает большие погрешности при малой вероятности р появления события А в одном испытании. В этом случае для подсчета вероятности Pn(m) удобно пользоваться формулой Пуассона, в которой следует положить  .
.
Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности  .
.
Пример 3. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0, 001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?
Решение:
Здесь  .
.
По формуле (17) находим

Распределение Пуассона часто встречается и в других задачах. Так, например, если телефонистка в среднем за один час получает N вызовов, то, как можно показать, вероятность Р(k) того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить  .
.
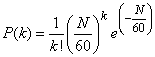
Если возможные значения случайной величины  образуют конечную последовательность x1, x2,..., xn, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой
образуют конечную последовательность x1, x2,..., xn, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой

и

Значения 
| x1
| x2
| ...
| xn
|
| Вероятности p(xi)
| p1
| p2
| ...
| pn
|
Эту таблицу называют рядом распределения случайной величины  . Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости.
. Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости.
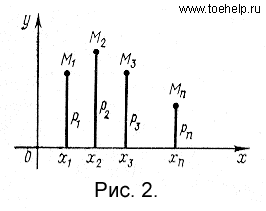
По горизонтальной оси будем откладывать возможные значения случайной величины  , а по вертикальной оси - значения функции
, а по вертикальной оси - значения функции  . График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
. График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
Пример 4. Пусть событие А — появление одного очка при бросании игральной кости; Р(A)=1/6. Рассмотрим случайную величину  — число наступлений события А при десяти бросаниях игральной кости. Значения функции р(х) (закона распределения) приведены в следующей таблице:
— число наступлений события А при десяти бросаниях игральной кости. Значения функции р(х) (закона распределения) приведены в следующей таблице:
Значения 
|
|
|
|
|
|
|
|
|
|
|
|
| Вероятности p(xi)
| 0, 162
| 0, 323
| 0, 291
| 0, 155
| 0, 054
| 0, 013
| 0, 002
|
|
|
|
|
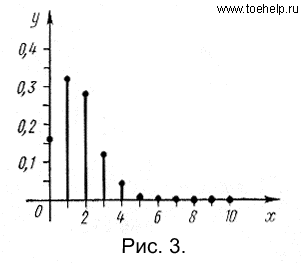
Вероятности p(xi) вычислены по формуле Бернулли при n=10. Для x> 6 они практически равны нулю. График функции p(x) изображен на рис. 3.
Дальше...
* Случайные величины будем обозначать малыми буквами греческого алфавита:  ,....
,....

 , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2,..., xn,.... Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1, 2,...) равно вероятности того, что величина
, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2,..., xn,.... Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1, 2,...) равно вероятности того, что величина 

 - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений
- число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений 

 .
. 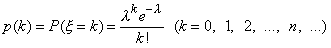
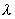 — некоторая положительная постоянная. В этом случае говорят, что случайная величина
— некоторая положительная постоянная. В этом случае говорят, что случайная величина  .
.  .
. .
.
 .
.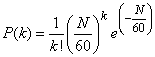




 ,....
,....


