Методика методу розділення перемінних
Крок 1. (Знаходження елементарних розв’язків рівняння з частковими похідними). Ми хочемо знайти функцію T(x, t), що є розв’язком задачі (1), (4) – (6). Будемо шукати розв’язок, представлений у вигляді (7). Для цього підставимо вираз (7) у рівняння (1). У результаті підстановки одержуємо
Тепер виконаємо операцію, властиву даному методу: розділимо обидві частини останнього рівняння на
Про цей вираз говорять, що в ньому з мінні розділені, тобто ліва частина рівняння залежить тільки від t, а права частина тільки від x. Тому що x і t не залежать один від одного, то кожна частина цього рівняння повинна бути константою. Позначимо цю константу k, тоді
Тепер можна вирішити кожне з цих звичайних диференціальних рівнянь. Добуток відповідних розв’язків буде задовольняти вихідному рівнянню з частковими похідними. (Помітимо, що ми істотно спростили вихідний розв’язок з частковими похідними другого порядку, перетворивши його в два звичайних диференціальних рівняння). Звернемо тепер увагу на наступну важливу обставину: константа поділу k повинна бути негативною [2] (іншими словами функції N(t) повинні прагнути до нуля при t ® ¥). Маючи це на увазі, введемо позначення k = - w2, де w не дорівнює нулю (у цьому випадку вираз - w2 буде завжди негативним). З урахуванням нового позначення для константи розподілення два звичайних диференціальних рівняння запишемо у вигляді
Отримані рівняння є стандартними звичайними диференціальними рівняннями. Їхні загальні розв’язки записуються у вигляді
де А, В, С – довільні постійні. Отже, функції виду
(де С1=А× В і С2 = А× С – довільні постійні) задовольняють рівнянню (1). Отже, ми одержали нескінченний набір функцій, що задовольняють вихідному рівнянню з частковими похідними. Крок 2. (Знаходження розв’язків, що задовольняють граничним умовам). Положення зараз таке: у нас є нескінченна безліч розв’язків вихідного рівняння, але не усі вони задовольняють граничним чи початковим умовам. Наступний крок складається у виборі такої підмножини розв’язку вигляду (15), що задовольняють граничним умовам (4) і (5). Щоб зробити це, підставимо розв’язок (15) у ці граничні умови. У результаті одержуємо
Друга гранична умова накладає обмеження на можливі значення константи поділу w: вона повинна бути коренем рівняння sinwl = 0. Іншими словами, щоб задовольнити умові
або
Відзначимо, що можна задовольнити другій граничній умові якщо покласти С1 = 0, але в такому випадку розв’язок (15) буде тотожно дорівнювати нулю. Отже, ми закінчили виконання другого кроку і маємо у своєму розпорядженні нескінченний набір функцій
кожна з який задовольняє рівнянню з частковими похідними і граничними умовами.[3] Розв’язок вихідної задачі буде являти собою деяку суму з цих найпростіших функцій. При цьому конкретний вигляд суми буде залежати від початкової умови. Крок 3. (Знаходимо розв’язок задовольняючого рівнянню, граничним і початковим умовам). Останній крок полягає в знаходженні такої суми фундаментальних розв’язків
тобто в підборі таких коефіцієнтів С1п, що функція буде задовольняти початковій умові (6). Підстановка (21) у (6) дає
Вираз (22) являє собою розкладання функції j(х) у ряд Фур'є, відповідно до якого вираз для коефіцієнта С1п має наступний вигляд
Підставляючи (23) у (21), одержуємо загальний розв’язок вихідної задачі:
Можна переконатися в тому, що отриманий нами розв’язок задовольняє всім умовам вихідної задачі. На цьому закінчується крок 3.
|

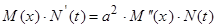 (9)
(9)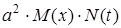 , у результаті чого одержуємо
, у результаті чого одержуємо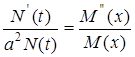 (10)
(10)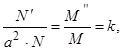 (11)
(11)
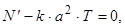
 (12)
(12) (13)
(13)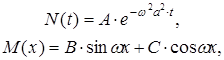 (14)
(14)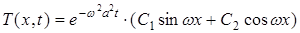 (15)
(15)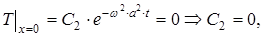 (16)
(16)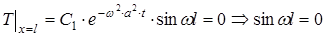 (17)
(17)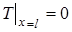 необхідно зажадати виконання співвідношень
необхідно зажадати виконання співвідношень , (18)
, (18)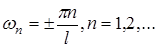 (19)
(19)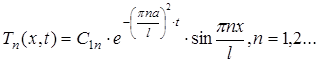 , (20)
, (20)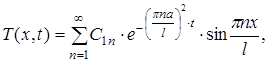 (21)
(21)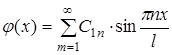 (22)
(22) (23)
(23)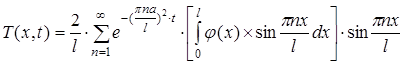 (24)
(24)


