Зробимо заміну змінних
Одержуємо
де Тепер для знаходження функції
Знайдемо
Інтегруючи праву частину (13) двічі по частинах і з огляду на (8) і (69), одержуємо
Таким чином, система рівнянь (6) – (9) переходить у наступне звичайне лінійне диференціальне рівняння 1-го порядку для функції FS(s, t):
Вирішуємо (15) – (16) методом Бернуллі: FS = m(t)× n(t) (17) Одержуємо для перебування функції n(t) диференціальне рівняння з поділяючими змінними
розв’язок якого має вигляд:
Аналогічно, для функції m(t):
де с – стала величина. Підставляючи (19) і (21) у (17) і враховуючи початкову умову (16), маємо
На другому етапі розвязування задачі для знаходження оригіналу Т(x, t) використовуємо зворотне синус-перетворення Фур'є для функції F(s, t):
Підставляючи (22) у (23), одержуємо
Внутрішній інтеграл I знаходимо методом інтегрування по частинах:
З використанням довідкової літератури одержуємо
Підставляючи (25) і (26) у (24) і з огляду на (5) і (10), знаходимо загальний розв’язок вихідної задачі
Якщо прийняти у формулі (27) Тn(t) = Tnл (температура плавлення матеріалу), то одержуємо
Отримана формула (28) дозволяє проводити розрахунки розподілів температури по глибині оброблюваного матеріалу (металу, скла та ін.) рухливим сканіруючим джерелом тепла (електронним променем, лазерним випромінюванням та ін.), що створює на поверхні оброблюваного виробу тонкий розплавлений шар товщиною порядку декількох мікронів. Задача2. При обробці виробу через його поверхню всередину матеріалу надходить тепловий потік Fn(t). Процес теплопередачі в цьому випадку описується наступним рівнянням теплопровідності з граничною умовою II-го роду на поверхні (Рис.4).
Рисунок 4 – Схема теплового впливу на оброблюваний виріб при заданому тепловому потоці на його поверхні Fп(t) (інші позначення аналогічні рис.3)
Необхідно, використовуючи метод інтегральних перетворень Фур'є, знайти загальний розв’язок задачі T(x, t).
Розв’язок Використовуючи заміну змінних (5), одержуємо
Для знаходження функції
З використанням (37) перетворимо систему рівнянь (33) – (36):
Інтегруючи (38) двічі по частинах, одержуємо
У результаті для перебування функції Fс(s, t) одержуємо наступне диференціальне рівняння
Для розв’язку задачі (40) – (41) використовуємо, також як і в попередній задачі, метод Бернуллі і одержуємо
На II-му етапі розв’язку задачі оригінал
Підставляючи (42) у (43), маємо
З використанням (5) і (26) одержуємо наступний загальний розв’язок задачі
За формулою (45) можна розраховувати значення температури в різних точках виробів, оброблюваних сканіруючими джерелами тепла різної природи, при заданих значеннях теплових потоків Fn(t). Задача 3 В процесі поверхневої обробки матеріалу в зоні впливу джерела тепла відбувається теплообмін з навколишнім середовищем за законом Ньютона. При цьому процес теплопровідності описується наступним рівнянням теплопровідності з граничною умовою III роду на поверхні (Рис.5)
Рисунок 5 – Схема конвективного теплообміну поблизу поверхні оброблюваного виробу
® - напрямок руху охолоджуваної рідини (газу) вздовж нагрітої поверхні з швидкістю W що має температуру Tc(t) < Ts (Ts – температура оброблювальної поверхні).(Інші позначення аналогічні рис.3).
Потрібно, використовуючи метод інтегральних перетворень Фур'є, одержати загальний розв’язок задачі T(x, t). Розв’язок Перетворимо систему рівнянь (46) – (49), зробивши наступні заміни
Одержуємо
Для знаходження функції
Далі за допомогою (55) перетворимо систему рівнянь (51)-(54):
Інтегруючи праву частину (56) двічі по частинах і з огляду на (53) і (54), одержуємо
Таким чином, для перебування функції Fsc (s, t) маємо наступне диференціальне рівняння
Розв’язуючи (58) – (59) одержуємо, також як і в попередніх задачах, методом Бернуллі:
На II-му етапі розв’язку задачі оригінал
Підставляючи (60) у (61), одержуємо:
  (62) (62)
Внутрішні інтеграли I1 і I2 знаходимо з довідникової літератури:

Підставляючи (63) і (64) у (62), одержуємо:
Внутрішні інтеграли в (65) обчислимо, використовуючи, відповідно до довідкової літератури, наступний вираз
З урахуванням (66) одержуємо:
 (67) (67)
Підставляючи (67) і (68) в (66) і з огляду на (50), одержуємо загальний розв’язок задачі
Формула (69) дозволяє розраховувати розподіл температури по глибині оброблюваних виробів, поблизу поверхні яких відбувається конвективний теплообмін з охолоджуючою рідиною.
|

 (5)
(5) , (6)
, (6)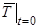 , = 0, (7)
, = 0, (7) , (8)
, (8) при х ® +¥, (9)
при х ® +¥, (9) (10)
(10) на I -му етапі розв’язку задачі використовуємо пряме синус-перетворення Фур'є по координаті х:
на I -му етапі розв’язку задачі використовуємо пряме синус-перетворення Фур'є по координаті х: (11)
(11) перетворивши (6) – (9) відповідно до (11):
перетворивши (6) – (9) відповідно до (11): , (12)
, (12) (13)
(13) (14)
(14)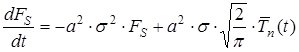 , (15)
, (15)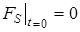 (16)
(16) , (18)
, (18)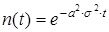 (19)
(19)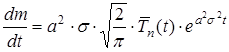 , (20)
, (20) , (21)
, (21) (22)
(22) (23)
(23)
 (24)
(24) (25)
(25)
 (26)
(26) (27)
(27) (28)
(28)
 , (29)
, (29) , (30)
, (30) , (31)
, (31) при х ® +¥ (32)
при х ® +¥ (32) , (33)
, (33) , (34)
, (34) , (35)
, (35) при х ® +¥ (36)
при х ® +¥ (36) (37)
(37) (38)
(38) (39)
(39) , (40)
, (40)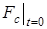 (41)
(41) (42)
(42) (43)
(43) (44)
(44) (45)
(45)
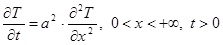 , (46)
, (46) , (48)
, (48) при х ® +¥ (49)
при х ® +¥ (49)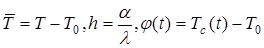 (50)
(50) , (51)
, (51) (53)
(53) при х ® +¥ (54)
при х ® +¥ (54) (55)
(55) (56)
(56) (57)
(57) (58, 59)
(58, 59) (60)
(60) (61)
(61)
 (65)
(65) (66)
(66)
 (68)
(68) (69)
(69)


